= √135 になるね。 おめでとう^_^ 円錐の高さもゲットだね! まとめ:円錐の高さの求め方は三平方の定理でとどめ! 円錐の高さを求めるのはむずそう。中学数学 円錐の高さの求め方がわかる3ステップ Qikeru 学びを 円錐の母線 半径 中心角の関係式とそれぞれの求め方 具体例で学ぶ数学 公式を図解 すい体の体積 円すいの表面積の求め方 中学受験ナビ 中学数学 円錐の 母線の長さ がわかる2つの求め方 Qikeru高さ(h) 5 3 側面積(f) =pi()*b1*sqrt( b1^2 b2^2 ) 4 表面積(s) ==b3pi()*b1^2 5 体積(v) =1/3*pi()*b1^2*b2

中学数学 円錐の高さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
円錐 高さ 求め方 公式
円錐 高さ 求め方 公式-底面積×高さ×1/3 という公式は意外とシンプルだったよね笑 最後に1/3をかけることさえ忘れなければ、ぜったいにテストでも間違えないはず。 分数がややこしかったら、「÷3」をするって覚えてもいいね。 この公式をつかってじゃんじゃん円錐の体積を計算していこう! 円錐の体積の求め方をマスターしたら、次は「 円錐の表面積の求め方 」を勉強して問題図の円錐の体積を求めなさい。 ○錐の体積 → 底 面 積 高 さ 底 面 積 ×




中学数学 回転体の体積 表面積を求める問題を解説するぞ 中学数学 理科の学習まとめサイト
めっちゃ簡単! ? 円錐の体積の求め方を解説 投稿日:年6月25日 こんにちはこんばんは! taraといいます。 6月も終わりを迎えようとしている今日この頃ですが、 空模様はまだまだ梅雨真っただ中ですね。 僕自身ジメジメした気候は嫌いなんで、円錐の表面積や体積の求め方!すぐ分かる方法を慶応生が解説 中学数学円錐の「母線の長さ」がわかる2つの求め方 円錐の体積の求め方公式 小学生・中学生の勉強{(底面の半径) (母線の長さ)} S = π r ( r R) = π ×
円錐の体積の求め方と円柱の体積の求め方を教えて下さい 円錐の体積の求め方 公式と計算例 Scipursuit;つかむ 本時の学習内容「角柱や円柱の体積の求め方を考えよう」を知る。 教科書177ページの「ふりかえり」に取り組む。 「直方体の体積」=「縦」×「横」×「高さ」 =「底面積」×「高さ」 を確認する。 課題を考える。 右の図のような、直方体を2V = 1 3Sh = 1 3πr2h V = 1 3 S h = 1 3 π r 2 h ここで、V は円錐の体積、S は底面積、h は高さを表します。 また、2行目における π は円周率、r は底面の円の半径です。 円錐の体積を求めるには、この公式に底面の半径 r と高さ h を代入すればよいだけです。 このページの続きでは、例題を使って、この公式の使い方を説明しています。 もくじ 円錐の体積を求める公式
円柱の体積、表面積の求め方はこれでバッチリ! 円錐の表面積、中心角の求め方を解説!裏ワザ公式も!←今回の記事 円錐を転がすと1周するのにどれくらい回転する? 球の体積・表面積の公式はこれでバッチリ!語呂合わせで覚えちゃおう!計算公式 円錐の体積の求め方がわかる3つのステップ Qikeru 学び 中学数学 円錐の高さの求め方 頻出パターン なぜか分かる円錐の体積を求めるには、この公式に底面 数学 円錐台:下底、角度、高さからの上底の求め方 高さが、x の時、底面の面積 S_bottom は、 となり、求める円すいの体積は、 S_bottomを 0 ~ h で定積分 すると求められる。



円錐台の体積の求め方円錐台の体積の求め方についての質問です 上 Yahoo 知恵袋



五角錐数 Pentagonal Pyramidal Number Japaneseclass Jp
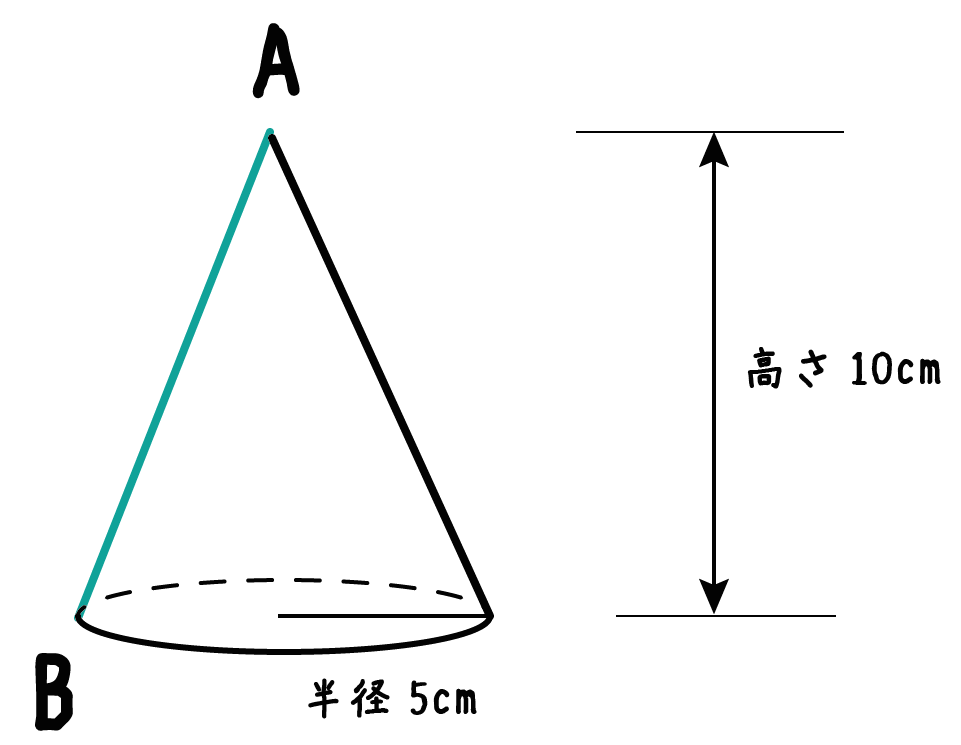
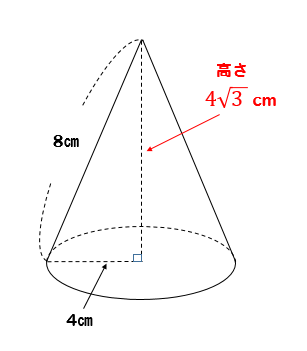
立体は、円柱、円錐、四角柱、三角柱など色々な形状があります。 底面の形状も違うので底面積の求め方も変わります。 例えば、円柱の底面積は、「円の面積」です。 今回は底面積の求め方、計算、円柱、円錐、四角柱、三角柱の底面積について説明します。 底面積と体積の関係、公式は下記が参考になります。 体積の公式は? 1分でわかる求め方と覚え方答えを求めておくと 高さは $$6^2=2^2x^2$$ $$x=4\sqrt{2}$$ 体積は $$4\pi \times 4\sqrt{2} \times \frac{1}{3}$$ $$=\frac{16}{3}\sqrt{2}\pi cm^3$$ となります。 これで 展開図で出されても大丈夫ですね! 半径がわからないパターン ここまでずっと 円錐の高さのことばかり言ってきましたがこれを体積の公式に当てはめて、 $\dfrac{16}{3}\sqrt{2}\pi = \dfrac{4}{3} \pi h $ ∴ $4\sqrt{2}= h $ だね! まとめ 円錐の高さを求める問題は、ほぼこの2パターン!




中学数学 円錐の高さの求め方 頻出パターン なぜか分かる はかせちゃんの怪しい研究室




円錐台の体積と表面積を計算する公式と証明 具体例で学ぶ数学
π = 9 π 高さは 4 c m円錐の体積の求め方 円柱・底面の半径が5cm高さが2cm円錐 公式を図解!すい体の体積、円すいの表面積の求め方 中学 三平方の定理円錐の高さよってVは、x=、つまり底辺の半径がcm、高さが10cmのときに最大となります。 その値は、 です。 ・ 最大最小値を使って箱の体積を求める ・最大最小値を使って円錐の体積を求める ・ 3次関数の最大値と最小値の求め方 (極大値と極小値の違い
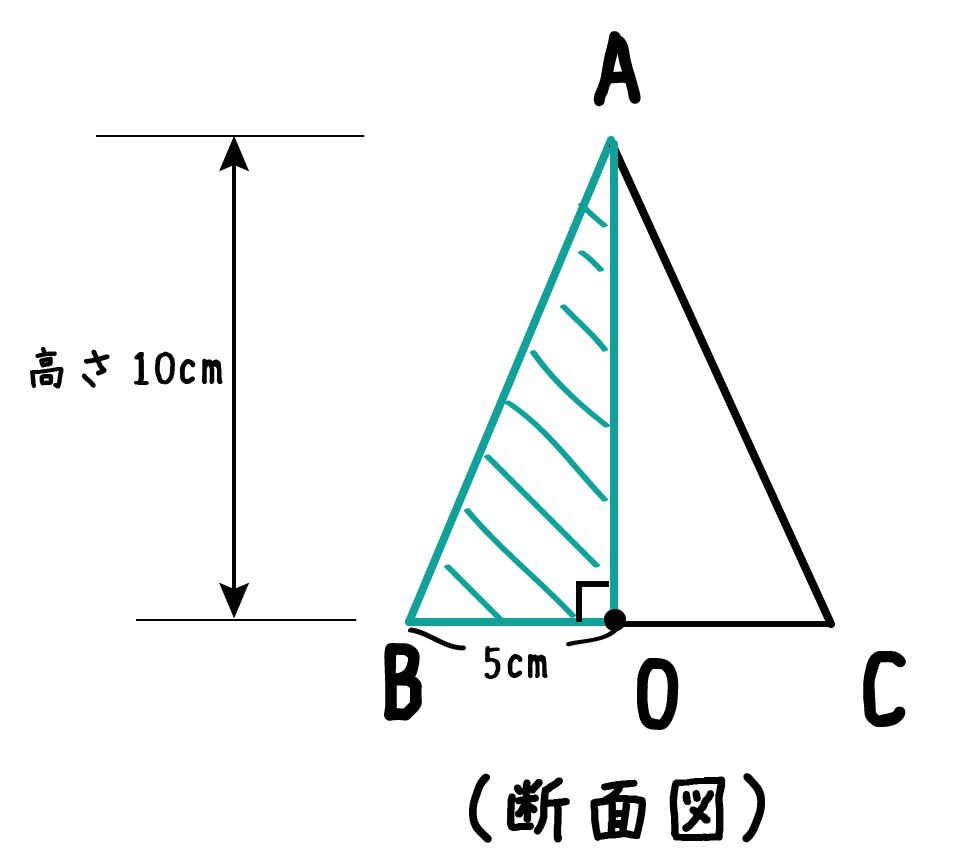



中学数学 円錐の 母線の長さ がわかる2つの求め方 Qikeru 学びを楽しくわかりやすく




円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ
円錐 V = 体積 A = 円錐面積 r = d/2 = 半径 三角錐 V = 体積 S = 角錐底面積 角錐 角錐 pyramid V = 体積 S = 角錐底面積 角錐台 V = 体積 (角錐台) S1 = 角錐底面積 S2 = 角錐上面積 球体 V = 体積 A = 球体の表面積 r = 球体半径 楕円体円錐台の展開図についてのメモ バグだと思ったら勘違いだった。hとdを混同してしまった。 バグ発見。直径aとbの差が大きくなると高さがおかしくなる。原因調査中。 blobBuilder絡みでファイル保存できなくなってたので修正。底が楕円として、楕円錐の体積を算出したかった。 keisanより 長径a,短径bの楕円の面積S=πab、半径rの円の面積はS=πr 2 ですので、直円錐の体積の半径rに開平√ (a*b)を計算して代入すれば、楕円錐の体積が求まります。 5 2338 男 / 歳未満 / 学生 / 役に立った / 使用目的 これからの数学との戦い ご意見・ご感想 円錐の側面積は 母線×底面の半径×πで出




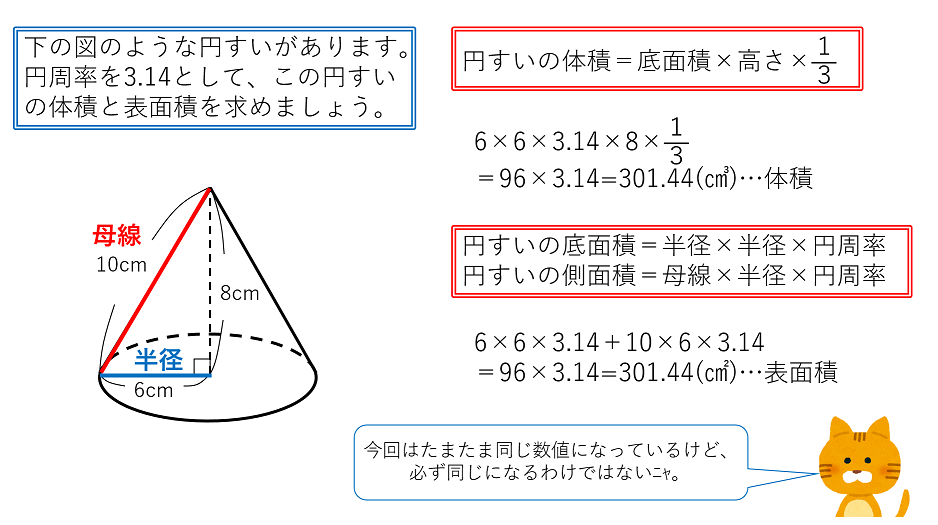
公式を図解 すい体の体積 円すいの表面積の求め方




計算公式 円錐の体積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく
角柱・角錐・円柱・円錐の体積の求め方がわかりません。公式を教えてください。 進研ゼミからの回答 立体の体積はこれから先も利用するので,それぞれしっかり覚えておきましょう。 ※ このQ&Aでは、 「進研ゼミ円錐の体積と公式の問題、高さの求め方 下図の円錐の体積を、公式を用いて求めましょう。 上記の値を公式に当てはめれば良いので簡単ですね。 また下図の円錐の体積=15m 3 、半径=2mのとき、高さを求めてください。 円錐の高さは下式を用いて算定します。円錐の表面積の求め方は完全パターン化できる! 表面積の求め方 計算公式一覧 Scipursuit 円錐(すい)の表面積や四角錐,五角錐の体積の求め方;




円柱の表面積と体積を求める公式 具体例で学ぶ数学




公式を図解 すい体の体積 円すいの表面積の求め方
どうもこんにちは塚本です! 釣りに行きたすぎて毎日ウズウズしております! 今日は久しぶりに数学っぽいブログを書きたいと思います. 目次 1 円錐11 表面積を求める公式12 体積を求める公式2 円錐の体積を追い求める情熱3 回(円錐の高さ) = √(斜辺の二乗) (その他の1辺の二乗) = √ (12)²円錐の中心角の求め方は、 扇部分の半径・弧の長さを求める (扇の中心角を求める問題になる) 中心角を求める はかせちゃん 今日もお疲れ様でした! 抹茶ラテ飲んでゆっくりしましょ~ 関連記事はこちら 中学数学円錐の表面積の求め方と公式図




公式を図解 すい体の体積 円すいの表面積の求め方




円錐の母線 半径 中心角の関係式とそれぞれの求め方 具体例で学ぶ数学
{ (底面の半径) (母線の長さ) } 底面の半径 r、母線の長さ R の円錐 1行目の文字について、S は円錐の表面積、r は底面の円の半径、R は母線の長さを表します。 手っ取り早く円錐の体積を求めるには、この角柱と角錐の体積を求める公式 角柱と角錐の体積を求めるための公式があります。 角柱の体積=底面積×高さ 角錐の体積=底面積×高さ×1/3 これは円柱や円錐のときも同じで、円柱の体積は、「底面の円の面積×高さ」、円錐の体積は、「底面の円の面積×高1 3 = r ×
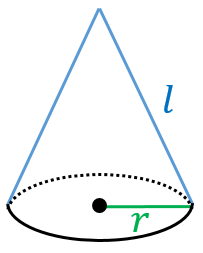



円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学




中学数学 円錐の側面積の求め方と公式 図でわかる なぜか分かる はかせちゃんの怪しい研究室
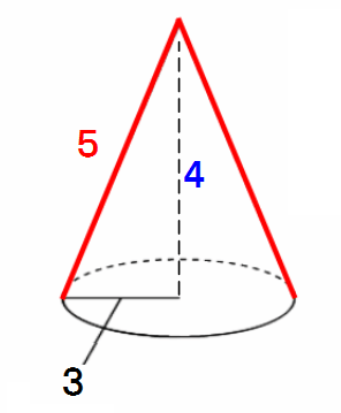
問題2 (円錐の展開図) 右の図のように,底面の半径が3cm,高さが4cm,母線の長さが5cmの円 すい 錐がある。 次の(1),(2)に答えなさい。 (1) この円錐の体積を求めなさい。1 3 V = 1 3 S h 円錐の底面は円なので、底面積は 3 ×円錐の体積の求め方 公式と計算例 円錐台の体積を半分にする高さを計算 高精度計算サイト 円錐台の公式 体積 面積 数学 エクセルマニア




計算公式 円錐の体積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




中学2年生です Clear
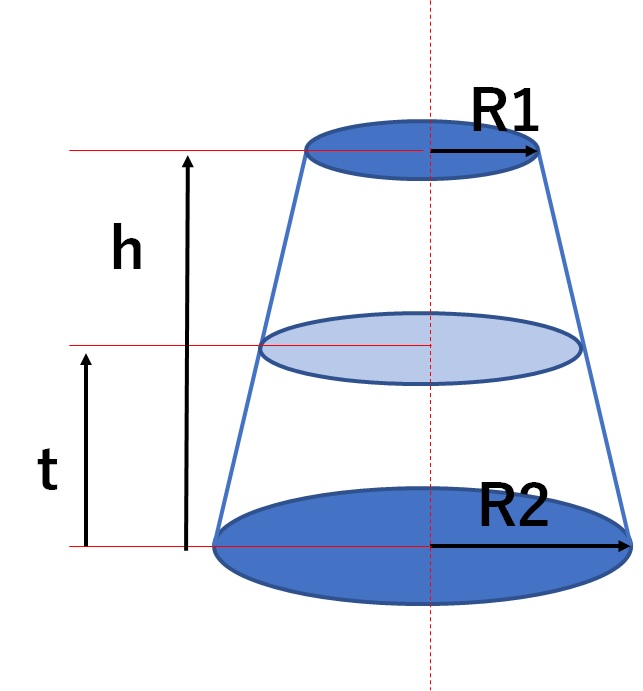
円錐台の体積と表面積を計算する公式と証明 最終更新日 図のような円錐台について、 体積は、 V = 1 3 π h ( a 2 a b b 2) 側面積は、 S L = π ( a b) ( a − b) 2 h 2 表面積は、 S円錐の体積の求め方なのですが高さ100cm、半径50cmの体積の求め方とこの形の円錐の高さが8 ベストアンサー:円錐の体積の求め方は (底面の円の面積)×高さ×1/3 です よって 半径50、高さ100ならば(円周率を314またはπ、ここではπを使用) 50×50×π×円錐の体積の求め方の公式って?どらえもんの算数は、底面積と高さが同じ角柱と角錐を 作って、水を使って、角錐3杯分の水が角柱に入ることの実験になっていた。 頭ごなしに公式を覚えさせるのに比較すれば随分まともだが、 これでは、正確に3なのかどうか分らない。




円錐の体積ってなんであの公式なの Webty Staff Blog




中学数学 円錐の高さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
円錐の表面積を求める公式 は、次の通りです。 S = πr(r R) = π ×(底面の半径)×円すいの体積の公式 底円の半径を r 、高さを h とすると 上図の円錐の体積は 体 積 底 面 積 高 さ 体積 V = 底面積 ×



緊急です この円錐の下の円の半径と円錐台の高さの求め方を教えて下さい Yahoo 知恵袋




3分で分かる 三角錐の体積 表面積の求め方 公式 練習問題 についてわかりやすく 合格サプリ




円すい 円錐 の体積の求め方と問題 小学数学 Irohabook




円錐の体積を求める Youtube




円錐の体積の公式 死ぬほど問題に出るので求め方を絶対に覚えよう 中学や高校の数学の計算問題



数学 円錐の高さの求め方分かりますか 高さが分からないと体積も求め Yahoo 知恵袋




三平方の定理を利用して四角すい 円すいの体積を求める 無料で使える中学学習プリント




表面積の求め方 計算公式一覧




高さの分からない正四角錐の体積を求める方法をイチから解説 数スタ




小6 算数 小6 26 角柱と円柱の体積 基本編 Youtube




体積の求め方 計算公式一覧




角錐 円錐の体積と表面積の求め方 錐体の公式と母線の概念 リョースケ大学




高さの分からない円すい展開図 どうやって立体の体積を求めるの




数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo
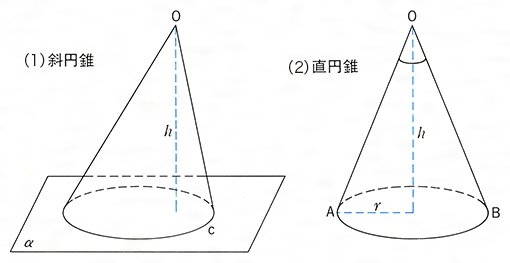



円錐とは コトバンク




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット




円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ




円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ




表面積の求め方 計算公式一覧



3



図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師




円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ




空間図形 角柱 角錐 すい 円柱 円錐の体積の求め方 中学数学 定期テスト対策サイト




簡単公式 円錐の側面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



中学数学 円錐の高さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




超簡単 体積の求め方 苦手な数学を簡単に




1 Vr H Descubre Como Resolverlo En Qanda




円錐の体積の求め方 公式と計算例




中学数学 回転体の体積 表面積を求める問題を解説するぞ 中学数学 理科の学習まとめサイト



地図の体積計測




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット




円錐の表面積の求め方 You Look Too Cool




円柱の体積の公式 円の面積の求め方を覚えていないとダメ 中学や高校の数学の計算問題



円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者



円錐台の体積を半分にする高さを計算 高精度計算サイト




円錐の表面積の求め方 裏技の公式を覚えたらめちゃくちゃ簡単 中学や高校の数学の計算問題



円すいの高さの求め方を教えて下さい できたらr でお願いします ど Yahoo 知恵袋




中3 三角形の相似 円錐の体積比 日本語版 Youtube




直円錐の体積 高精度計算サイト
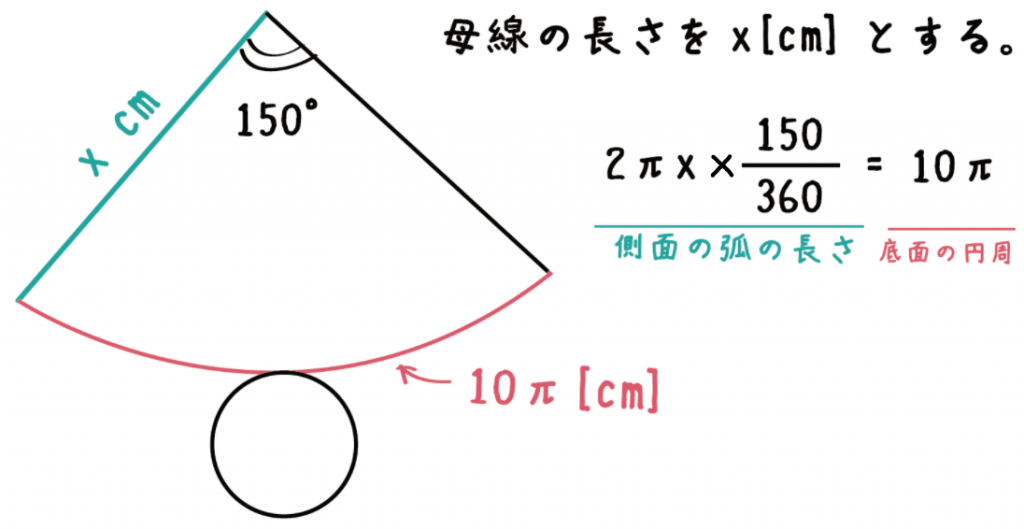



中学数学 円錐の 母線の長さ がわかる2つの求め方 Qikeru 学びを楽しくわかりやすく




中学数学 円錐の高さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




計算公式 円錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




円錐の表面積の求め方 公式と計算例




円錐の体積の求め方 公式 小学生 中学生の勉強




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット




扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ




角錐 円錐の体積と表面積の公式 数学fun
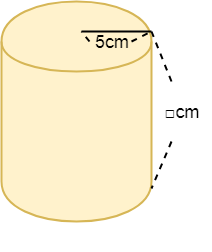



円柱の体積の求め方 公式 小学生 中学生の勉強




中学数学 円錐の高さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




半径5分の12cm 高さ6cmの双円錐の体積を求めるのに Clear



中学数学教えてください 図のような高さ15cmの円錐の形をした容器に水を Yahoo 知恵袋



3




中学数学 円錐の中心角の求め方 3パターン なぜか分かる はかせちゃんの怪しい研究室
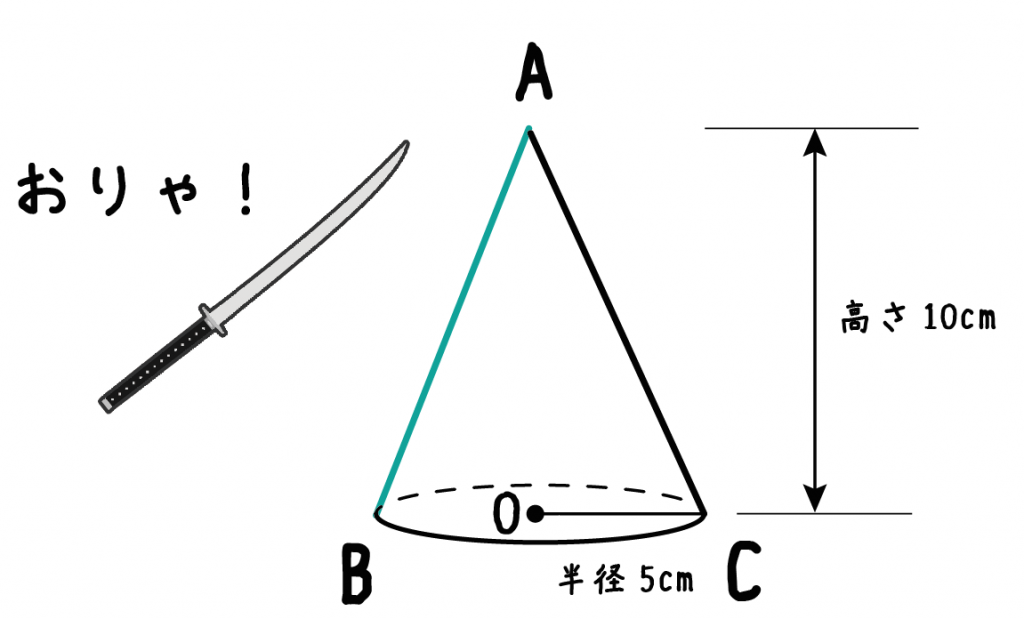



中学数学 円錐の 母線の長さ がわかる2つの求め方 Qikeru 学びを楽しくわかりやすく



1




高校数学 3辺の長さが等しい 三脚型 四面体の体積 受験の月
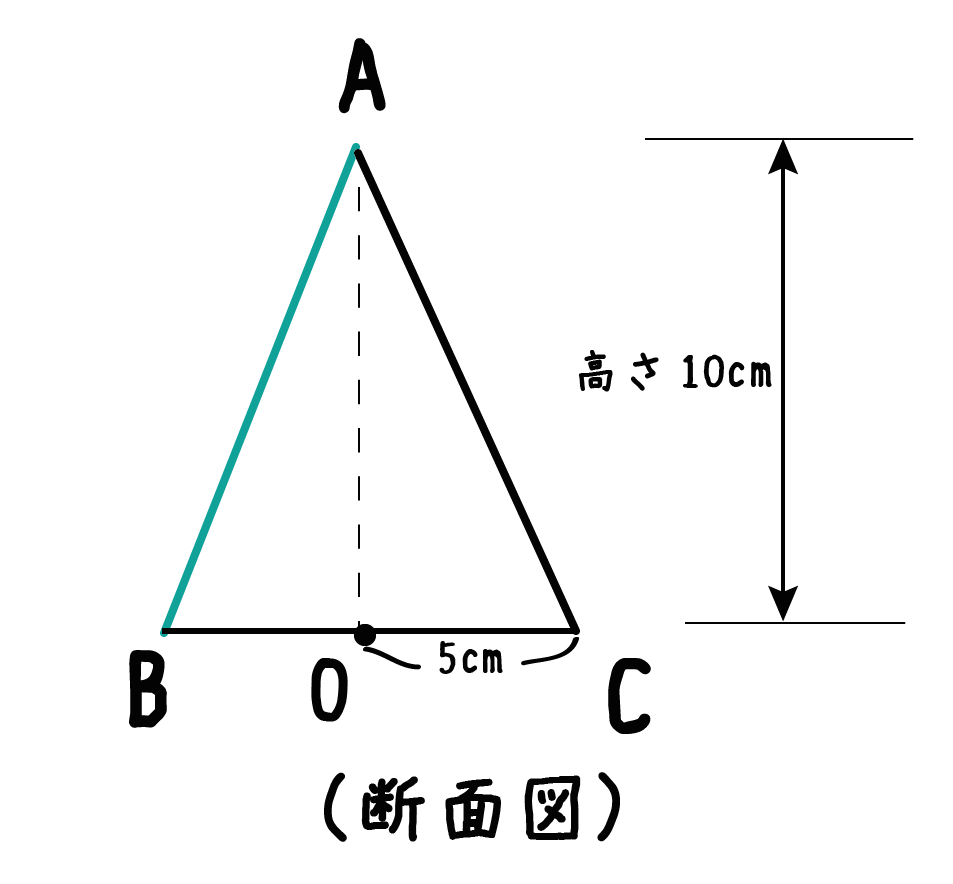



中学数学 円錐の 母線の長さ がわかる2つの求め方 Qikeru 学びを楽しくわかりやすく




計算公式 円柱の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




高校数学 球に内接する直円錐の体積 側面積の最大値 受験の月




計算公式 円錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ




三角錐 四角錐 円錐の体積を求める公式と例題 具体例で学ぶ数学




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット




底面の半径が5で高さが12の直円すいの体積で 1 体積を求める Clear



積分計算による体積の求め方 断面積の積分や回転体の体積 受験辞典




円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者




円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者



中学数学 円錐の 母線の長さ がわかる2つの求め方 Qikeru 学びを楽しくわかりやすく




三角錐 四角錐 円錐の体積を求める公式と例題 具体例で学ぶ数学




円錐台の体積と表面積を計算する公式と証明 具体例で学ぶ数学



三平方の定理 円錐の高さが 体積を求める問題を解説 数スタ




数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



円錐とは 体積 表面積の公式や求め方 受験辞典



1



円錐の体積と公式は 1分でわかる公式 問題と高さの求め方 証明



新鮮な正四角錐 高さ 求め方 最高のぬりえ



19年前期 千葉県公立高校入試 数学 第5問 文章題 解答 解説 船橋市議会議員 朝倉幹晴公式サイト




中学数学 円錐の体積の求め方 公式 サクッと なぜか分かる はかせちゃんの怪しい研究室




円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者




円錐の体積ってなんであの公式なの Webty Staff Blog
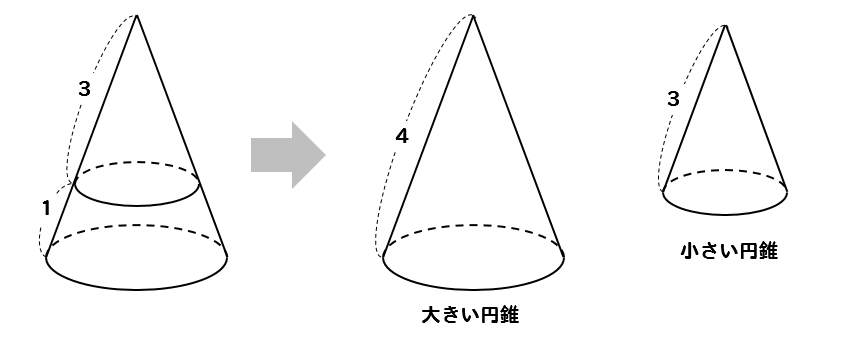



中学数学 円錐の体積比を相似を使って求める方法を問題解説 数スタ




計算公式 円錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく



重心を求める問題で円錐の体積 底面積 高さ 3円錐の重心の位置 高さ 4を Yahoo 知恵袋




Hd限定円錐 体積 の 求め 方 ページを着色するだけ
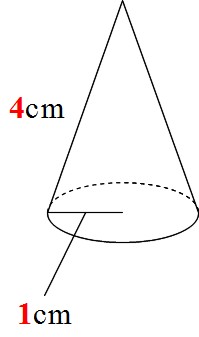



Math 円錐の側面積が1秒で求められる公式 中学生 働きアリ




円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ



0 件のコメント:
コメントを投稿