X/2 y = 6;5x – 1 = 3y asked in Linear Equations by Anika01 (Find the value of x and y using cross multiplication method 6x y = 18 and 5x 2y = 22

Ch1 Linear Equation In Two Variables
X y/2=4 x/3 2y=5 by cross multiplication method
X y/2=4 x/3 2y=5 by cross multiplication method- Solve, using crossmultiplication 5x 4y 14 = 0 3x = 10 – 4y Answer Given equation are 5x 4y 14 = 0 and 3x = 10 – 4y Comparing with a 1 x b 1 y c 1 = 0 and a 2 x b 2 y c 2 = 0, We have a 1 = 5, b 1 = 4, c 1 = 14 and a 2 = 3, b 2 = 4, c 2 = 10 Question 5 Solve, using crossmultiplication x – y 2 = 0 7x 9y = 130Methods to Solve Simultaneous Linear Equations We have four important methods to solve simultaneous equations They are comparison, substitution, elimination, and crossmultiplication Out of all these methods, the simplest methods will effectively solve the equations and get the




Solve The Following System Of Equations By Method Of Cross Multiplication 2x Y 6 X Y 2
Cross multiplication method is the same as the Cramer's rule applied to )(b)a(1/b) =(b/a)(a/b)=(b^2 a^X Y 2 4 X 3 2y 5 By Substitution Method X Y 2 4 X 3 2y 5 By Substitution Method 3 Multivariable Calculus Limit Of X 2y X 2 Y 2 Using Polar Coordinates Calculus Math Videos Coordinates Systems Of Equations Elimination Worksheet Lovely Solving Systems By Elimination Worksheet In Systems Of Equations Solving Equations EquationsUsing cross multiplication method, Answer x = 3 and y = 2 Question 11 From equation (2) a 2 = a, b 2 = – b and c 2 = – 2ab Using cross multiplication method, we get RS Aggarwal Solutions for Class 10 Maths Chapter 3 Linear Equations in Two Variables Answer x = b and y = a
Show Graphically that the System of Equations X 2y = 5, 3x 6y = 15 Has Infinitely Many SolutionsΔ = b 2 4ac Δ = 10 2 4·2·(3) Δ = 124 The delta value is higher than zero, so the equation has two solutions We use following formulasCorrect answer to the question Slove the cross multiplication method 5/x4/y=2;2/x3/y=13 studyassistantincom
EduRev Class 10 Question is disucussed on EduRev Study Group by 596 Class 10 Students 04x 03y=17 07x02y=08 7(y 3)2(X 2)=14 4(y2) 3(x3)=2 X y/2=4 X/3 2y=5 solve this in two minHowever, the method of cross multiplication is applicable only when we have a pair of linear equations in two variables Consider that a 1 x b 1 y c 1 = 0 and a 2 x b 2 y c 2 = 0 are two equations that need to be solved By the method of crossmultiplication, we would find the values of the x and y variablesQuestion 10 Solve the following equations by the method of crossmultiplication 2x 3y = 9 3x 4y = 5 Solution Given linear equations are 2x 3y = 9 3x 4y = 5 Comparing with the standard form, a 1 = 2, b 1 = 3, c 1 = 9 a 2 = 3, b 2 = 4, c 2 = 5 Using crossmultiplication method, x/(b 1 c 2 – b 2 c 1) = y/(c 1 a 2 – c 2 a 1) = 1/(a 1 b 2 – a 2 b 1)




Ex 3 5 3 Solve By Substitution And Cross Multiplication Teachoo



Method Of Cross Multiplication Solve By Method Of Cross Multiplication
Step by step solution of a set of 2, 3 or 4 Linear Equations using the Substitution Method xy/2=4;x/32y=5 Tiger Algebra Solver 3x 2y = 4 Solution Substituting this value of y in equation (1), we obtain ∴ x = 2, y = 5 Crossmultiplication method Concept Insight In order to solve the given pair of equations by cross multiplication method, remember the formula to be used and convert the system of equations to standard formSteps for Solving Linear Equation x2y=5 x 2 y = 5 Subtract x from both sides Subtract x from both sides 2y=5x 2 y = 5 − x Divide both sides by 2 Divide both sides by 2




Systems Of Equations With Elimination X 2y 6 4x 2y 14 Video Khan Academy




0 4x 0 3y 1 7 0 7x 0 2y 0 8 7 Y 3 2 X 2 14 4 Y 2 3 X 3 2 X Y 2 4 X 3 2y 5 Solve This In Two Min From Substitution Elimination And Cross Multiplication Method Edurev Class 10 Question
Solve this by cross multiplication method 2(ax by) a 4b = 0 2(bxay) b 4a = 0 For what values of a the following pair of equation 4x3y=3 and 8xay=5 will have a unique solution Without drawing graph, check whether the lines 3x y = 10 and 6xFind the solution of x and y using cross multiplication method 3x y = 1 and x 2y = 5 x = 4, y = 1 WARNING!




Solve 3x 2y 11 And 2x 3y 4



Cross Multiplication Method Formula For Cross Multiplication Linear Equations
Now multiply equation (1) by 5 and (2) by 7 By adding both the equations Substitute the value of x in equation (1) Therefore, x = 7 and y = 2 If x = 7 and y – 2 satisfy the equation (3) then we can say that the equations hold simultaneously Substitute the value of x and y in equation (3) 43 = 43 which is trueX=3/2X5 We move all terms to the left X(3/2X5)=0 Domain of the equation 2X5)!=0 X∈R We get rid of parentheses X3/2X5=0 We multiply all the terms by the denominator X*2X5*2X3=0 Wy multiply elements 2X^210X3=0 a = 2;Solve each of the following systems of equations by the method of crossmultiplication x 2y 1 = 0 2x 3y 12 = 0 asked Apr 26 in Linear Equations by Haifa (




X Y 6 X Y 2 By Elimination Method Novocom Top




Chapter 5 Simultaneous Linear Equations Ml Aggarwal Icse Solutions For Class 9 Maths
Solve for x and y by cross multiplication method asked in Important Questions by ajaykr Premium (3 points) 0 votes 1 answer Solve the following equations (x/3) – 21/2 = 4x/9 – 2x/3 asked in Class VIII Maths by aditya23 (2,137 points) Using cross multiplication method, we get 2x−5y=4 (1) 3x−8y=5 (2) 8× (1)−5× (2) gives us, x=7 substitute the value of x in eqn (1), we get, y=2 Example 5 Solve the following system of equations by crossmultiplication method x y = a – b;




Maths Mania52 Equations Applied Mathematics



How To Solve 1 X 1 Y 7 2 X 3 Y 17 Where X And Y Is Not Equal To 0 By Cross Multiplication Method Quora
`x y/2 = 4` (i) `x/3 2y = 5` (ii) From (i), we get `(2x y)/2 = 4` 2x y = 8 y = 8 2x From (ii), we get x 6y = 15 (iii) Substituting y = 8 2x in (iii), we get x 6(8 2x) = 15 `=> x 48 12x = 15` => 11x = 15 48 => 11x = 33 `=> x = (33)/(11) = 3` Putting x = 3 in y = 8 2x we get y = 8 2 x 3 = 8 6 = 2 y = 2Given system is (1/x) (1/y) = 7 (1) (2/x) (3/y) = 17 (2) For doing it by cross multiplication method there's an easy pattrern , by which From substitution, elimination,and cross multiplication method?




Maths Class 10 Pages 51 100 Flip Pdf Download Fliphtml5




Solve The Following Pair Of Linear Equation Bycross Multiplication Method X 2y 2 X 3y 7
PreAlgebra Solve for x 2yx=3 2y − x = 3 2 y x = 3 Subtract 2y 2 y from both sides of the equation −x = 3 −2y x = 3 2 y Multiply each term in −x = 3−2y x = 3 2 y by −1 1 Tap for more steps Multiply each term in − x = 3 − 2 y x = 3 2 y by − 1 1In Maths, cross multiplication method is used to solve linear equation in two variables This is the simplest method and gives the accurate value of the variables Cross multiplication is only applicable when we have a pair of linear equations in two variables Let us suppose that a1x b1y c1 = 0 and a2x b2x c2 = 0 are the two equations which has to be solved = 1 Hence, = 1 x = 2 and, = 1 y = 5 Hence, the required solution is x = 2 and y = 5 Question 4 Form the pair of linear equations in the following problems and find their solutions (if they exist) by any algebraic method




Selina Chapter 6 Linear Equations Including Problems Icse Solutions Class 9 Maths




Rd Sharma Solutions For Class 10 Maths Chapter 3 Pair Of Linear Equations In Two Variables Updated For 21 22 Coolgyan Org
The procedure to use the cross multiplication calculator is as follows Step 1 Enter the fractions with the unknown value "x" in the respective input field Step 2 Click the button "Calculate x " to get the outpute Step 3 The unknown value "x" will be displayed in the output field "x"Answer to Solve 3 x 4 y = 10 and 4 x 3 y = 5 by the method of cross multiplication By signing up, you'll get thousands of stepbystepSolve the pair of equation by cross multiplication method 2/x 3/y = 13 5/x 4/y = 2 Solution Let 1/x = a And 1/y = b So the eqn becomes 2a3b =13 5a4b = 2 So, 2a3b13 = 0 5a4b2 = 0 Now by cross multiplication method we have the formula = = We have




Ncert Class 10 Chapter 3 Pair Of Linear Equations In Two Variables
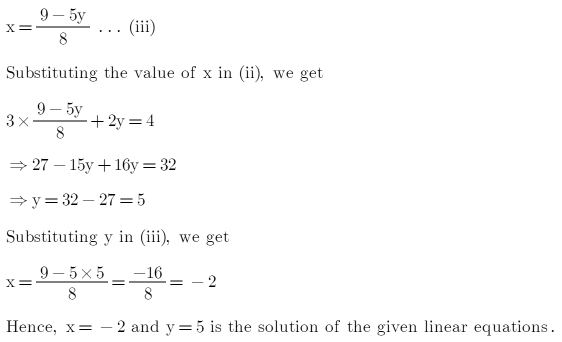



By The Substitution Method Solve The Linear Equation That Is 8 X 5 Y Is Equal To 9 And 3 X 2 Y Is Equal To 4 Mathematics Topperlearning Com Usvpr6ll
Ax – by = a 2 b 2 Sol The given system of equations can be rewritten as x y – (a – b) = 0 ax – by – (a 2 b 2) = 0 Using formula for cross multiplication method So, from equation (1) and (2) we can write the value of a,b and cLet x and y be two pipes So in 1 hour quantity of water filled by pipe x is 1/x and that of pipe y is 1/y The quantity of water filled by both pipes in one hour is 1/x 1/y It takes 24 hours by pipes to fill the pool So, 1/x 1/y = 1/24(1) The quantity of water filled in 8 hours by pipe A = 8/ASolve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more




X 7 Y 3 5 X 2 Y 9 6 By Elimination Method Novocom Top




X Y 6 X Y 2 By Elimination Method Novocom Top
Example 17 Solve the pair of equations 2/𝑥 3/𝑦=13 5/𝑥−4/𝑦=−2 2/𝑥 3/𝑦=13 5/𝑥−4/𝑦=−2 So, our equations become 2u 3v = 13 5u – 4v = –2 Hence, our equations are 2u 3v = 13 (3) 5u – 4v = – 2 (4) From (3) 2u 3v = 13 2u = 13To ask Unlimited Maths doubts download Doubtnut from https//googl/9WZjCW Solve by cross multiplication `x2y1=0 `, `2x3y12=0`Solving Linear Equations by Cross Multiplication Method Here is an example Suppose that we have to solve the following pair of equations \\begin{array}{l}2x 3y 11 = 0\\3x 2y 9 = 0\end{array}\ Our solution equality will be of the following form, where we have to figure out the question marks




Solve The Pair Of Equations 2 X 3 Y 13 5 X 4 Y 2 Youtube




無料ダウンロード 3x 2y5 X5 Y
Solve the following pair of linear equation by cross multiplication method x 4y 9 = 0;Graph y=2(x3)^24 Find the properties of the given parabola Tap for more steps Use the vertex form, , to determine the values of , , and Multiply by Simplify by adding and subtracting Tap for more steps Subtract from Add and The final answer is The value at isFind an answer to your question cross multiplication method find x and y xy/2=4 ;




100以上 Solve By Substitution Method X Y 14 X Y 4 Solve By Substitution Method X Y 14 X Y 4




Coss Multiplication Method For Solving Linear Equations Ncert 10
To ask Unlimited Maths doubts download Doubtnut from https//googl/9WZjCW Solve `3xy2=0 , 2xy8=0` by method of cross multiplication 3x 2y = 5; Transcript Example 7 Solve the following pair of equations by substitution method 7x – 15y = 2 x 2y = 3 7x – 15y = 2 x 2y = 3 From (1) 7x – 15y = 2 7x = 2 15y x = (𝟐 𝟏𝟓𝒚)/𝟕 Substituting the value of x in (2) x 2y = 3 (2 15𝑦)/7 2𝑦=3 Multiplying both sides by 7 7 × ((2 15𝑦)/7) 7×2𝑦=7×3 (2 15y) 14y = 21 15y 14y = 21 – 2 29y = 21 – 2




Simultaneous Linear Equations Class 9th Concise Selina Icse Maths Icsehelp




15 X Y 2 X Y 1 X 10 Y 2 Xy X 15 Y 6 Xy
In case there is a unique solution, find it by using cross multiplication method (i) x 3y 3 = 0, 3x 9y 2 = 0 (ii) 2x y = 5, 3x 2y = 8 (iii) 3x 5y = , 6x 10y = 40 (iv) x 3y 7 = 0, 3x 3y 15 = 0 SOLUTION Soln (i) For x 3y 3 = 0, 3x 9y 2 = 0 a 1 = 1, b 1 = 3, c 1 = 3, a 2 = 3, b 2 = 9, c 2 = 2 ∴ TheWhich of the following pairs of linear equations has unique solution , or infinity many solutions In case there is a unique solution , find it by using cross multiplication method x − 3 y − 3 = 0 3 xSlove 3 X 2 Y = 4 and X 2 Y = 5 by cross multiplication method, substitution method and elimination method Maths Pair of Linear Equations in Two Variables




Solve X Y 7 And 3x 2y 11




How To Solve By Cross Multiplication For X By 2 Ax By A 4b 0 2 Bx Ay B 4a 0 Quora
Y – 8 = x;Ex9 Solve by crossmultiplicaiton method x 2y 1 = 0 and 2x – 3y – 12 = 0 Sol We have,x 2y 1 = 0 and 2x – 3y – 12 = 0 By crossmultiplication method, we have Hence the solution is x = 3 and y = –2 Ex10There Are Actually 4 methods of solving this We have, 2x 3y = 11(i) and, 5x 2y = 18(ii) i) Elimination Method First choose which variable you want to eliminate I'm going with y So, Multiply the eq(i) with 2 first It will turn into, 4x 6y = 22(iii) Now, Multiply the eq(ii) with 3




क र स ग ण पद धत द व र सम करण क न म न प रण ल क हल कर 3x




7 Y 3 2 X 2 14 4 Y 2 3 X 3 2 Youtube
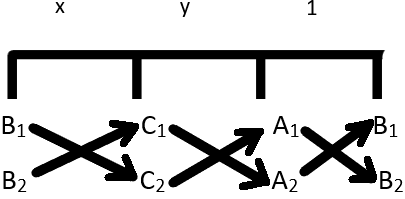
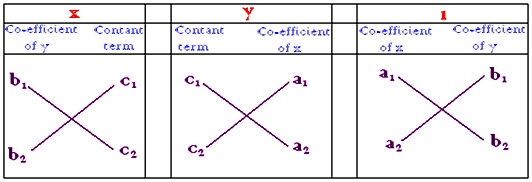
Class 10 Maths Linear Equations in 2 Variables Cross Multiplication Method Cross Multiplication Method Let's assume that we have to find solution for a 1 x b 1 y c 1 = 0 (i) and a 2 x b 2 y c 2 = 0 (ii) Step 1 Multiply Equation (i) by b 2 and Equation (ii) by b 1, to get b 2 a 1 x b 2 b 1 y b 2 c 1 = 0 (iii)X – y 1 = 0;Solve the following system of equations using cross multiplication method (i) 3 x 4 y = 24, x 11 y = 47 Solution (ii) 05 x 08 y = 044 , 08 x 06 y = 05 Solution (iii) (3x/2) (5y/3) = 2 , (x/3) (y/2) = 13/6 Solution (iv) (5/x) (4/y) = 2 , (2/x) (3/y) = 13 Solution Formulate the following problems as a pair of equations




X 2y 2x 3y 7solve By Cross Multiplication Method Brainly In



Linear Systems With Multiplication Algebra Socratic




Mathsmentor Answers Page 32 Ask Truemaths




2x Y 3 0 4x Y 3 0 By Cross Multiplication Novocom Top




Rd Sharma Solutions For Class 10 Chapter 3 Pair Of Linear Equations In Two Variables



Q Tbn And9gcryrp1jbmoopn8o27 Mhtryowbkwcuxnlgq44yonmvecxjmxl Usqp Cau




Solve The Pair Of Linear Equation By Cross Multiplication Method 5x 4y 4 0 X 12y 0 Brainly In




Selina Chapter 6 Linear Equations Including Problems Icse Solutions Class 9 Maths




Coss Multiplication Method For Solving Linear Equations Ncert 10




Solve The Pair Of Linear Equations By Cross Multiplication Method 2 2x Y 5 3 X 3y 1 0 Brainly In




Solve The Following Equation Using Cross Multiplication Method 7x 9y 19 0 And 4x 5y 21 0 Brainly In




Rd Sharma Solutions For Class 10 Maths Chapter 3 Pair Of Linear Equations In Two Variables Free Study Material Cbse Sample Papers Books Studyguide360



Q Tbn And9gcqpt2b1vv70to Lfdbr3ccujmyvr Vdkumxv5jjwr7ln1ajiae7 Usqp Cau
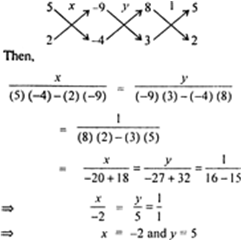



Solve The Following Pair Of Linear Equations By The Substitution And Cross Multiplication Methods 8x 5y 9 3x 2y 4 Zigya
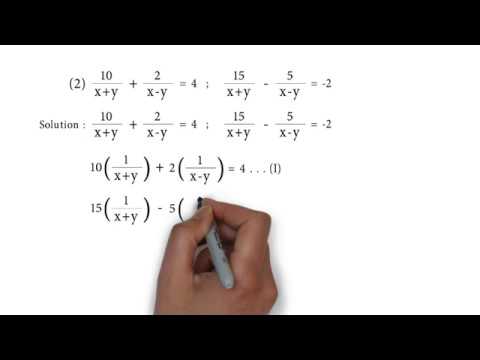



10 X Y 2 X Y 4 And 15 X Y 5 X Y 2 P S 1 4 Q2 Linear Equation In Two Variables Youtube




Solve The System Of Eq 2x 3y 17 3x 2y 6 By Method Of Cross Multiplication Brainly In




Pair Of Linear Equations In Two Variables Equations Cbse Class 10 Ekshiksha



Solve The System Of Equations By Using The Method Of Cross Multiplication X 6 Y 15 4 X 3 Y 12 19 4 Sarthaks Econnect Largest Online Education Community




Ch1 Linear Equation In Two Variables



Cbse 10 Math Cbse Linear Equations In Two Variables Ncert Solutions




Coss Multiplication Method For Solving Linear Equations Ncert 10




2x Y 2 X 3y 15 By Elimination Method



Solve The Following Systems Of Equations 10 X Y 2 X Y 4 15 X Y 5 X Y 2 Sarthaks Econnect Largest Online Education Community




R D Sharma Solutions Class 10th Ch 3 Pair Of Linear Equations In Two Variables Exercise 3 4




Chapter 6 Simultaneous Linear Equations Including Problems Selina Concise Mathematics Part I Solutions For Class 9 Mathematics Icse Topperlearning



Cbse 10 Math Ncert Solutions




Ch1 Linear Equation In Two Variables



Solve The Following Systems Of Equations 3 X Y 2 X Y 2 9 X Y 4 X Y 1 Sarthaks Econnect Largest Online Education Community




123a Ppt All 2




Example 18 Solve 5 X 1 1 Y 2 2 6 X 1 3 Y 2 1 Examples



Important Questions For Class 10 Maths Chapter 3 Pair Of Linear Equations In Two Variables Learn Cbse




無料ダウンロード 3x 2y5 X5 Y



Pair Of Linear Equations In Two Variables




R D Sharma Solutions Class 10th Ch 3 Pair Of Linear Equations In Two Variables Exercise 3 4




Solve The Following System Of Equations By Method Of Cross Multiplication 2x Y 6 X Y 2




2x 5y 4 And 3x 2y 16 0 Find X And Y Brainly In



Solve The Following Systems Of Equations X Y 2 4 X 3 2y 5 Sarthaks Econnect Largest Online Education Community



Q Tbn And9gctoh2pwk9b Efut7bzpd5lcbfmxewmaq29gbegj 1bsfatvupvw Usqp Cau




Cbse Ncert Solution For Class 10 Maths Linear Equations In 2 Variables




Ncert Class 10 Chapter 3 Pair Of Linear Equations In Two Variables




Ncert Solutions For Class 10 Maths Chapter 3 Pair Of Linear Equations In Two Variables Ex 3 5




15 X Y 2 X Y 1 X 10 Y 2 Xy X 15 Y 6 Xy




R D Sharma Solutions Class 10th Ch 3 Pair Of Linear Equations In Two Variables Exercise 3 3




Solve The Following Pair Of Linear Equations By The Substitution And Cross Multiplication Methods 8x 5y 9 3x 2y 4




Solve The Following Pairs Of Equation By Cross Multiplication Method 0 3 X 0 4 Y 2 5 And 0 5 X 0 3 Y 0 3




R D Sharma Solutions Class 10th Ch 3 Pair Of Linear Equations In Two Variables Exercise 3 3




Cross Multiplication Method For Solving Equations A Plus Topper




2x A Y B 2 X A Y B 4 By Cross Multiplication Novocom Top




Mp Board Class 10th Maths Solutions Chapter 3 Pair Of Linear Equations In Two Variables Ex 3 5 Mp Board Solutions




Simultaneous Linear Equations Popular Questions Icse Class 9 Math Mathematics Meritnation




Solve This By Cross Multiplication Method 2 Ax By A 4b 0 2 Bx Ay B 4a 0 Mathematics Topperlearning Com K2zyk5cc



Systems Of Linear Equations




Ex 3 4 1 Solve By Elimination And Substitution I X Y 5 2x 3y




Cbse Ncert Solution For Class 10 Maths Linear Equations In 2 Variables
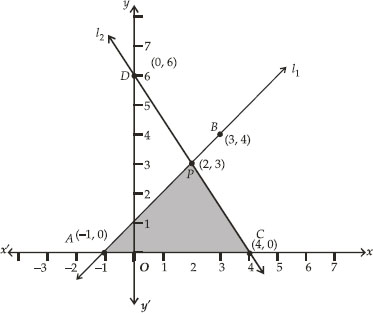



Ncert Solutions Pair Of Linear Equations In Two Variables Class 10




Ex 3 6 1 V And Vi 7x 2y Xy 5 8x 7y Xy 15



How To Solve A B X A B Y 2ab B2 A B X Y B2 By Cross Multiplication Method Studyrankersonline




Cross Multiplication Method For Solving Equations A Plus Topper




Gseb Solutions For Class 10 Mathematics Pairs Of Linear Equations In Two Variables Cbse Tuts
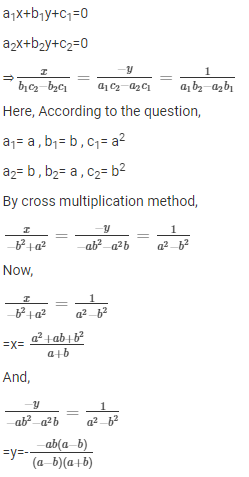



Rd Sharma Solutions For Class 10 Maths Chapter 3 Pair Of Linear Equations In Two Variables Free Study Material Cbse Sample Papers Books Studyguide360



Solve The Following Systems Of Equations 1 2 X 2y 5 3 3x 2y 3 2 5 4 X 2y 3 5 3x 2y 61 60 Sarthaks Econnect Largest Online Education Community



Solve The Following Systems Of Equations 1 2 X 2y 5 3 3x 2y 3 2 5 4 X 2y 3 5 3x 2y 61 60 Sarthaks Econnect Largest Online Education Community



How To Solve The Following Simultaneous Equations By Elimination Method A 2x 3y 12 X Y 1 B 3x Y 10 C X 3y 1 3x 2y 4 0 D 5 Quora




8x 5y 9 And 3x 2y 4 By Cross Multiplication Method Brainly In



Search Q 2x 2by 3d5 3x 2b2y 3d8 By Cross Multiplication Tbm Isch




How To Solve By Cross Multiplication For X By 2 Ax By A 4b 0 2 Bx Ay B 4a 0 Quora




123a Ppt All 2



How To Solve Following System Of Simultaneously Linear Equations Quora
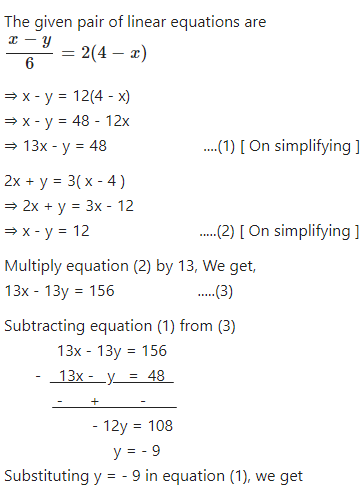



Simultaneous Linear Equations Class 9th Concise Selina Icse Maths Icsehelp




R D Sharma Solutions Class 10th Ch 3 Pair Of Linear Equations In Two Variables Exercise 3 4



Solve The Following Systems Of Equations X Y 2 4 X 3 2y 5 Sarthaks Econnect Largest Online Education Community



Solve 5 X 1 1 Y 2 2 And 6 X 1 3 Y 2 1 Studyrankersonline




Class Ten Maths Ncert Chapter 3 Solutions Freeguru Helpline
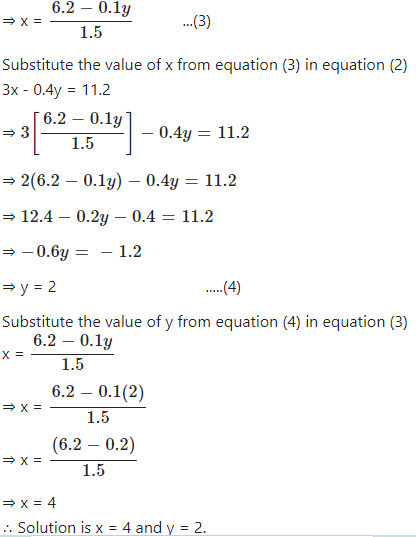



Simultaneous Linear Equations Class 9th Concise Selina Icse Maths Icsehelp




By Solving Equation 3x 4y 25 And 4x 3y 24 With The Help Of Cross Multiplication Method We Obtain Xa Yb 1c Then The Value Of A Is Equal To




Ex 3 5 3 Solve By Substitution And Cross Multiplication Teachoo



0 件のコメント:
コメントを投稿