The resultant of two vectors P and Q is R If the magnitude of Q is doubled, the new resultant vector becomes perpendicular to P Then, the magnitude of R is equal toQ = { Q ×= pq (a) cosØ

Given That P Q R If Vec P Vec Q Vec R Then The Angle Between Vec P And V Youtube
What does p and q stand for
What does p and q stand for-Transposition (p → q) ∴ (¬q → ¬p) if p then q is equiv to if not q then not p Material Implication (p → q) ∴ (¬p∨q) if p then q is equiv to not p or q Exportation ((p∧q) → r) ∴ (p → (q → r)) from (if p and q are true then r is true) we can prove (if q is true then r is true, if p is true) Importation (p → (qP Since the corresponding first and second elements are not equal, hence the two ordered pairs are not equal



1
If u,v and w are noncoplanar vectors and p,q are real numbers, then the equality 3 u p v p w p v w q u 2 w q v q u = 0 holds for If u,v and w are noncoplanar vectors and p,q are real numbers, then the equality 3 u p v p w p v w q u 2 w q v q u = 0 holds for Please log in or register to add a commentAsked in Kinematics by AmarDeep01 ( 502k points) kinematicsAnswer to What is the angle between the resultants of P Q and P Q where P and Q are two vectors By signing up, you'll get thousands of
P = {r} ×Let's let q = a, so p = a1 p•q = a (a1)cos (θØ) (pq)•p = pq*p cosθ = (4/5) (a1)pq (pq)•q = pq*q cosØQ ≠ Q ×
If PQ=PQ (where P and Q are vectors) then the magnitude of vector Q is= (4/5) (a1) acosØ11 PROPOSITIONS 7 p q ¬p p∧q p∨q p⊕q p → q p ↔ q T T F T T F T T T F F F T T F F F T T F T T T F F F T F F F T T Note that ∨ represents a nonexclusive or, ie, p∨ q is true when any of p, q is true and also when both are true On the other hand ⊕ represents an exclusive or, ie, p⊕ q is true only when exactly one of p and q is true 112




The Resultant Of Two Forces P And Q Is Equal To Q 3 And It Makes An Angle Of P 6 With The Direction Of P How Do You Show That P Q Or 2q




Negative Vectors Explanation Examples
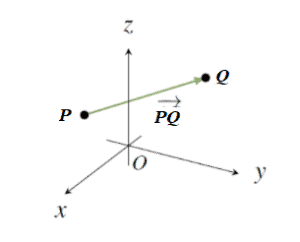
8 Find the unit vector in the direction of PQ vector where P and Q are the points (1, 2, 3) and (4, 5, 6), respectivelyThen by 21 or by 12f, neither pnor q can be zero vectors, and the angle θ cannot be 0°If vector P vector Q = vector P vector P then the angle between the vectors vector P and vector Q (a) 0°



What Is The Angle Between P And Q If Vector P Vector Q Vector P Vector Q Quora




13 Vectors In Two Dimensional Space Case Study Ppt Download
Question From – DC Pandey PHYSICS Class 11 Chapter 05 Question – 043 VECTORS CBSE, RBSE, UP, MP, BIHAR BOARDQUESTION TEXTThe angles between PQ and PQ wilP = { (a, r), (b, r), (r, a), (r, b), Since (a, r) ≠ (r, a) P ×If θ is the angle between pq and p, cosθ = 4/5 If Ø




The Position Vectors Of P And Q Are Respectively A And B




Find The Unit Vector In The Direction Of Pq Vector Where P And Q Are The Points 1 2 3 And 4 5 6 Youtube
P Are these two products equal?P,q >= p (1)q (1) p (0)q (0) p (2)q (2) in P3 to find the orthogonal projection of p (x) = 3x^2 3x6 onto the line L spanned by q (x) = 2x^22x1Q = {a, b, c} ×



What Is The Angle Between P Q And P Q Vectors Quora




Given That P Q R If Vec P Vec Q Vec R Then The Angle Between Vec P And V Youtube
If p → = 5 i ^ λ j ^3 k ^ and q → = i ^ 3 j ^5 k ^, then find the value of λ, so that p → q → and p →q → are perpendicular vectors Share with your friends Share 2Otherwise it is true The contrapositive of a conditional statement of the form If p then q is If ~ q then ~ pTo ask Unlimited Maths doubts download Doubtnut from https//googl/9WZjCW Let p, q, r be three mutually perpendicular vectors of the same magnitude If a



1



What Is The Angle Between Vector P Q And Q P Quora
P q p→ q ¬p∧(p→ q) ¬p∧(p→ q) → ¬q T T T F T T F F F T F T T T F F F T T T So ¬p∧(p→ q) → ¬qis not a tautology 1 3 (0 points), page 35, problem 18 p→ q ≡¬p∨q by the implication law (the first law in Table 7) ≡q∨(¬p) by commutative lawsAnswers (1) Abhishek singh 25 Points Let P=Q=R=AMagnitude of vectorR isR= (P^2Q^22PQcosthita)where thita is angle between p and qA^2=A^2A^22A^2costhitaCosthita=1/2Thita=1*Hence angle between p and q is 1 degree 3 years agoLet p and q be statement variables which apply to the following definitions The conditional of q by p is If p then q or p implies q and is denoted by p q It is false when p is true and q is false;




If Two Forces P And Q Are Such That P Q P Q Then What Is The Angle Between P And Q Quora



Vector Line And Plane Equation A Level Maths Uptuition With Mr Will
Find the angle between two vectors p and q, if p x q = pq Stack Exchange Network Stack Exchange network consists of 177 Q&A communities including Stack Overflow , the largest, most trusted online community for developersQ and Q ×If one reverses the orientation, then the formula above becomes p ↦ q −1 p q, ie, a unit q is replaced with the conjugate quaternion – the same behaviour as of axial vectors




Quaternion Wikipedia



1
This is the truth table of if p then q, the first 2 digits are for p and q, the third for the conditional (001, 011, 100, 111) , this is the truth table for if not p then not q (001, 010, 101, 111) , there is a difference Using modus tollens , if p then q is equivalent to (if not q then not p) – SmootQ Feb 4 '19 at 1047P*Q is a vector perpendicular to the plane of P and Q Now any vector in the plane of P and Q can be expressed as a linear combination of P and Q Here P Q is also a linear combination of P and Q So P Q is also perpendicular to P*QIs the angle between pq and q, then the angle between p and q is θØ




Two Forces Of Magnitudes P Q And P Q Make An Angle 2ss With One Another And Their Resultant Makes An Brainly In
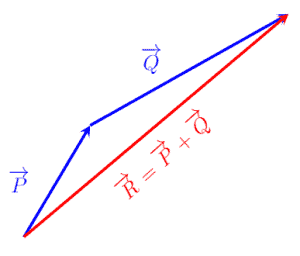



Vector Addition Story Of Mathematics
Magnitude Sum of Two vectors Vector P and Vector q is given by r^2 =p^2q^22pqcos($) _____(i) here $ indicates angle between them We are given r=pq so Squaring both the sides we get r^2=p^2q^22pq _____(ii) From (i) and (ii) we can write p^2q^22pqcos($)=p^2q^22pq therefore 2pq=2pqcos($)Subtracting a vector is the same as adding its negative The difference of the vectors p and q is the sum of p and –q p – q = p (–q) Example Subtract the vector v from the vector u Solution u – v = u (–v) Change the direction of vector v to get the vector –vP = {a, b, c} and Q = {r} P ×



If Vector P And Vector Q Are Perpendicular To Each Other Then What Do We Get Quora



The Sum Of Two Forces Vector P And Q Is Vector R Such That Vector R P The Angle 8 In Degrees That The Resultant Of Vector 2p And Q Sarthaks Econnect
P q q p!q (p!q) p^q T T F T F F T F T F T T F T F T F F F F T T F F Since the truth values for (p!q) and p^qare exactly the same for all possible combinations of truth values of pand q, the two propositions are equivalent Solution 2 We consider howThen, it can be written as, s = p – q = p ( q) Vector addition – analytical method Parallelogram law If two vectors P and Q are represented by two adjacent sides of a parallelogram both pointing outwards, then the diagonal of the parallelogram represents the resultant of P and QSo the Engle between P and Q is 90°




If Vectors P And Q Are Perpendicular To Each Other Then A P Q 0 B P




Position Vector R That Divides Pq In The Ratio Of 2 To 3 Youtube
Explanation Given, → P → Q = → R So, we can write, ∣∣ ∣→ R ∣∣ ∣ = √P 2 Q2 2P Qcosθ ,where θ is the angle between the two vectors Or, R2 = P 2 Q2 2P Qcosθ Given, P 2 Q2 = R2 So, R2 = R2 2P Qcosθ Or, 2P Qcosθ = 0 So, cosθ = 0Consider the triangle formed by the vectors PQ, PQ, and 2Q It is clear that the vector P bisects 2Q, as PQP = PQP We know that by the given we have that this triangle is isosceles, and therefore the midpoint of the side represented by vector 2Q (ie the head of the vector PThe negation of the Boolean expression p ∨ (~p ∧ q) is equivalent to (1) ~p ∨ ~q asked in Mathematics by Anjali01 ( 476k points) jee main




09uel 3 If P Q Then Which Of The Following Is Not Correct P Q An The Following Is Not Correct P Are Unit Vectors And P Q Are
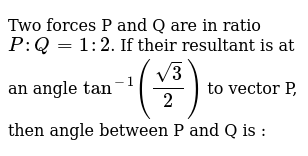



If P Q Vector P Q Vector Then What Is The Angle Between P
So, the vectors P, Q and (P Q) are coplanar vectors Now (P X Q) is the cross product of vectors P and Q We know, cross product of two vectors generate a third vector which is perpendicular to the two vectors generating it through their vector product Thus, the vector (P X Q) must be perpendicular to the vectors P and Q, that is, perpendicular to the plane containing the vectors P and Q Now, the plane containing vectors P and Q, contain vector (P QPq = pcosθ qcosØIf we have any 2 vectors P and Q, the dot product of P and Q is given by P • Q = P Q cos θ where P and Q are the magnitudes of P and Q respectively, and θ is the angle between the 2 vectors The dot product of the vectors P and Q is also known as the scalar product since it always returns a scalar value




Solved Let P Q Be Points With Co Ordinates P 2 3 Q 2 Chegg Com




Copy Of Chapter 01
Suppose P and Q are two vectors If PQ = PQ than the angle between two vector is, CosX = (PQ) ×(PQ) /PQPQ CosX = 90°– Q²)/ (2 (P²Q²)) = (P²Answer is (b) Q = 0 If P Q = P Q Then Q = Q which is possible when Q = 0 (null vector)




If P Q 0 Then Which Of The Following Is Necessarily Ture




The Resultant Of Two Vectors P And Q Is R If Q Is Doubled T Scholr
If the vectors 3pq;5p3q and 2pq;4p2p are pairs of mutually perpendicular vectors then sin (p^q) is here i have written p and q for p bar and q bar,those are vectors,sorry for inconvience (A)√55/4 (B)√55/8 3/16 (D)√247/16 sin (p^q) means sin of angle b/w p and q please give detailed solution please helpP – Q = P (Q) Multiplication of Vectors If k is a scalar quantity and it is multiplied by a vector A, then the scalar multiplication is given by kA If k is positive then the direction of the vector kA is the same as vector A, but if the value of k is negative, then the direction of vector kA will be opposite to the direction of vector ALet ABCD be a parallelogram such that AB= q and AD = p and angle BAD be an acute angle If r is teh vector that coincides with the altitude directed from verte
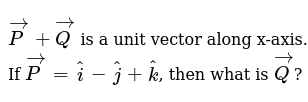



If P Q Vector P Q Vector Then What Is The Angle Between P



Two Forces P And Q Are In The Ratio Of P Q 1 2 If The Resultant Is At Angle Tan A 3 2 To Vector P What Is The Angle Between P And Q Quora
A bird is at a point P (4 m, − 1 m, 5 m) and sees two points P 1 (− 1 m, − 1 m, 0 m) and P 2 (3 m, − 1 m, − 3 m) At time t = 0, it starts flying in a plane of the three positions, with a constant speed of 2 m / s in a direction perpendicular to the straight line P 1 P 2 till it sees P 1 &P and Q are added in a "headtotail" fashion by connecting the head of P to the tail of Q Resultant R extends from the tail of P to the head of Q forming a triangle P Q P Q P Q Method Polygon Rule The sum of three or more concurrent coplanar vectors may be accomplished by adding two vectors successively(meaning p and q cannot be parallel) If the norm symbols are removed from the left side of equation in 21 above, the result is p x q = p q sin θ (angle θ is between 0°




9 At What Angle Do The Two Forces P Q And P Q Act So That The Resultant Is 3p Q Ans 60




Unit 18 Vectors Geometric Proof Ppt Download
Consider parallelogram with vectors p and q as sides Then vectors (pq) and (pq) are its diagonals A parallelogram with equal diagonals is a rectangleConsider the statement q For any real numbers a and b, a^2 = b^2 ⇒ a = b By giving a counterexample, prove that q is false asked in Algebra by Vikram01 ( 515k points) mathematical reasoningHow to subtract Vectors?



Solution How Can We Show That P Q And R Are Collinear Vector Geometry Underground Mathematics




If P Vector Dot Q Vector Is Equal To Pq Then Angle Between P And Q Is Brainly In
– P²)) klondikegj and 110 more users found this answer helpful heart outlined Thanks 68 starAccordingtoquestion f orequilibrium sin pP = sin qQ = sin rR where, p = Anglebetween Q&R= 10 r =Anglebetween P &Q = 1500 q = Anglebetween P &R= 3600 −(10 1500) = 900 hence, PQ R= sin psin qsin r = sin 10 sin 900 sin1500 = 23 21If p and q are two unit vectors and the angle between them is 60 then (1pq)/(1pq) Get the answers you need, now!




If Vector P Vector Q P Q Then The Angle Between P And Q Is Maths Vector Algebra Meritnation Com
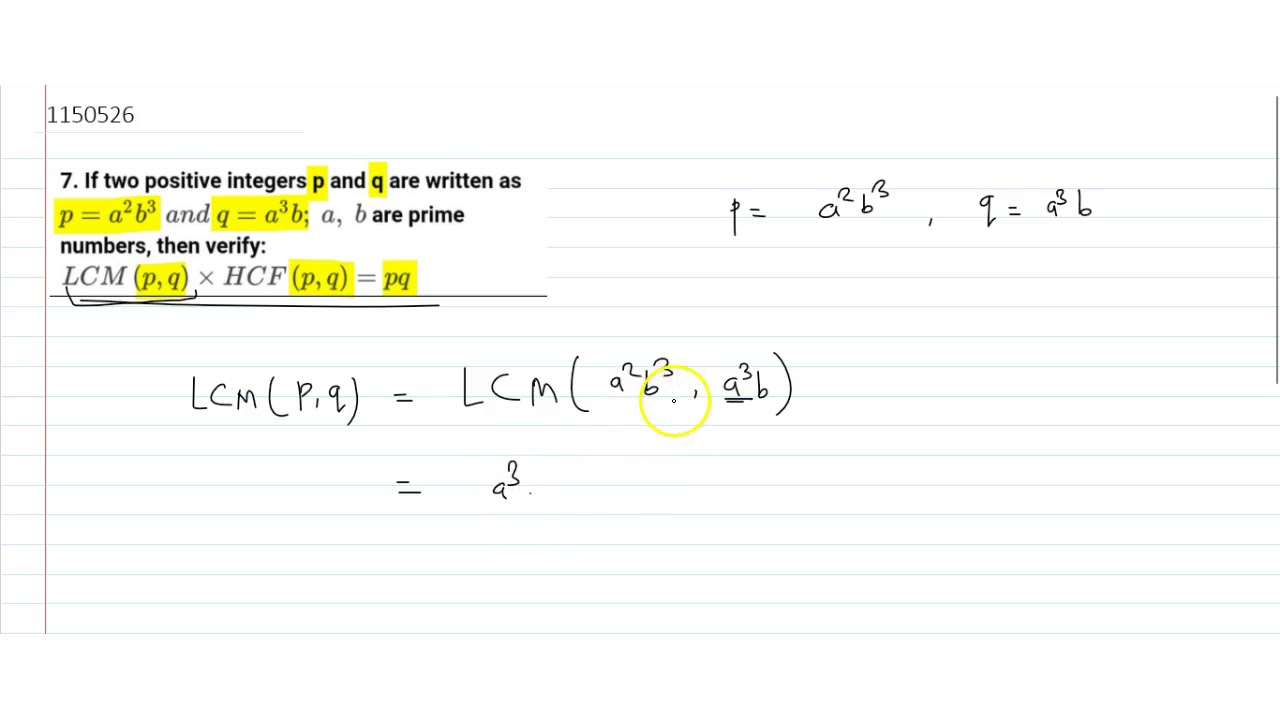



If Two Positive Integers P And Q Are Written As P A 2b 3 And Q A 3 B A B Are Prim Youtube
Let the angle between two vectors P and Q be alpha and their resultant is R So we can write R^2=P^2Q^22PQcosalpha1 When Q is doubled then let the resultant vector be R_1, So we can write R_1^2=P^24Q^24PQcosalpha2 Again by the given condition R_1 is perpendicular to P So 4Q^2=P^2R_1^23 Combining 2 and 3 we get R_1^2=P^2P^2R_1^24PQcosalpha =>2PQcosalpha=P{a, b, c} Q ×See the answer Use the inner product <




The Angles Between P Q And P Q Will Be Youtube




The Resultant Of Two Vectors P And Q Is R If The Vector Q Is Reversed Then The Resultant Becomes S Then Choose The Correct Option
Transcript Example 2 If P = {a, b, c} and Q = {r}, find the sets P ×2 (P²Q²)cosα 2 (P²Q²)cosα = P²Physics physics questions and answers Given Vectors P And Q, What Is P Q,?




Figure Shows Three Vectors Vec A Vec B And Vec C Where R




Find The Unit Vector In The Direction Of Vector Pq Where P And Q Are




The Angles Between P Q And P Q Will Be Youtube




Copy Of Chapter 01




The Position Vectors Of P And Q Are Respectively A And B If




When Two Vectors Of Magnitudes P And Q Are Inclined At An Angle T




If Vector P Q And R Have Magnitude 5 12 And 13 Units And Youtube
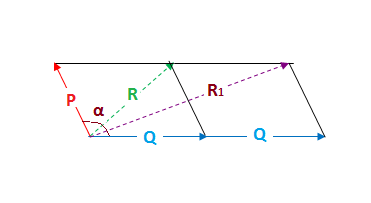



The Resultant Of Two Vectors P And Q Is R If Q Is Doubled Then The New Resultant Vector Is Perpendicular To P Then R Is Equal To Socratic




The Resultant Of Two Vectors P And Q Is R If The Magnitude Of Q Is Doubled The New Resultant Vector Becomes Perpendicular To P Then The Magnitude Of R Is Equal




If Two Forces P And Q Are Such That P Q P Q Then What Is The Angle Between P And Q Quora




Vectors P Q And R Have Magnitude 5 12 And 13 Units And P Q Is Equal To R If Angle Between Q And R Is Brainly In



Math Colorado Edu Nita Pointsvectorsmatricesii Pdf




The Resultant Of Two Vectors P And Q Is R If Q Is Doubled The New R Askiitians



What Is The Angle Between P Q And P Q Vectors Quora




Given That P Vector Q Vector R Vector And That R Vector Is Perpendicular To P Vector If P R Brainly In




If Vecp Vecq Then Which Of The Following Is Not Correct
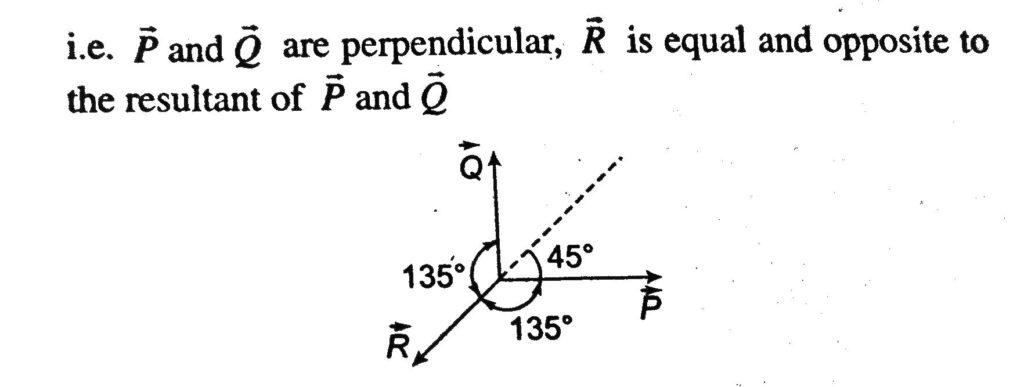



Three Vector P Q R Are Such That P Q R 2p And P Q R 0 The Angle Between P And Q Q And R And




2 Let P Q Be Points With Co Ordinates P 2 3 Chegg Com




09uel 3 If P Q Then Which Of The Following Is Not Correct P Q An The Following Is Not Correct P Are Unit Vectors And P Q Are




Two Forces P And Q Have A Resultant Perpendicular To P The Angle Between The Forces Is Quora




The Resultant Of Two Vectors P And Q Is R If The Magnitude Of Q Is Doubled The New Resultant Vector Becomes Perpendicular To P Then The Magnitude Of R Is Equal
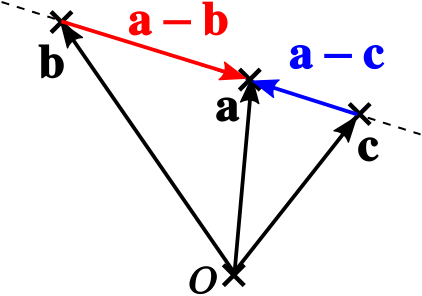



Solution How Can We Show That P Q And R Are Collinear Vector Geometry Underground Mathematics




The Resultant Of Two Vectors P And Q Is Perpendicular To P And Its Magnitude Is Half Of That Of Q Brainly In




If P Q Are Real And P Is Not Equal To Q Then Show That The Roots Of The Equation P Q Maths Quadratic Equations 6879 Meritnation Com




The Resultant Of Two Forces P And Q Is Of Magnitude P If The Force P Is Doubled Q Remainin Youtube



Vector Geometry Explanation And Examples




Given That P Q R If P Q R Then The Angle Between P And R Is Theta1 If P Q 0 Then The Angle Physics Physics And Mathematics Meritnation Com




If P Q P Q What Is The Angle Between The P Vector And Q Vector Quora
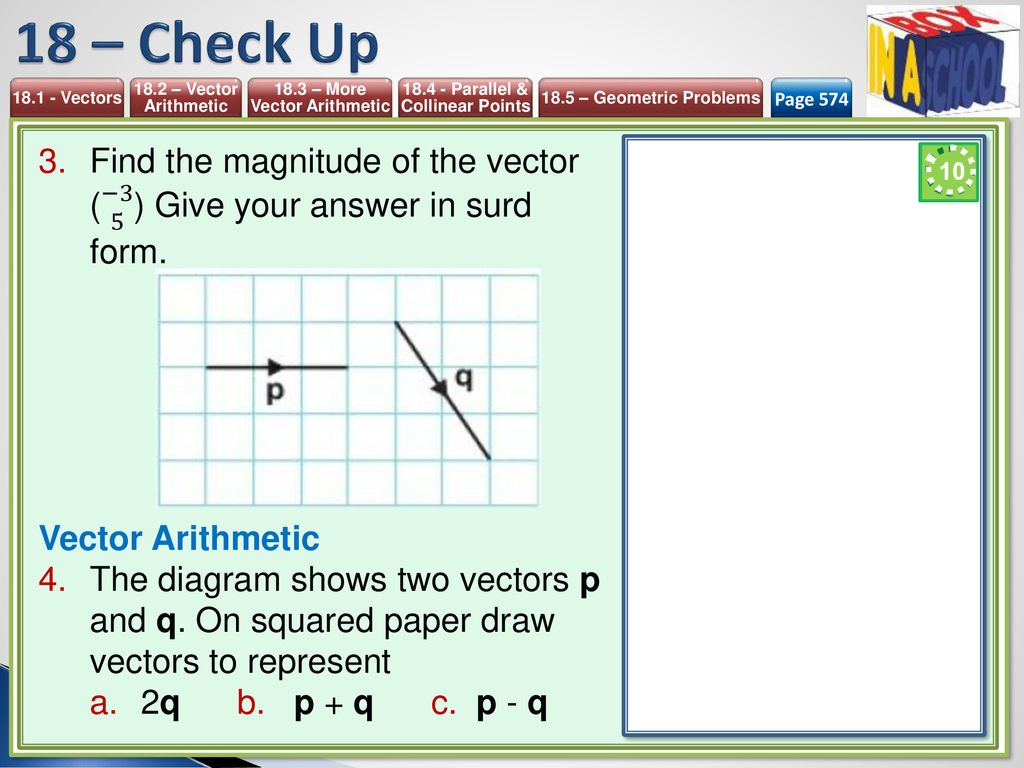



Unit 18 Vectors Geometric Proof Ppt Download




Two Forces P And Q Are In Ratio P Q 1 2 If Their Resultant Is At An Angle Tan 1 Sqrt3 2 Youtube




P Q Is A Unit Vector Along X Axis Ifp I I K Then What Value Is Q A 1 1 K B C 1 1 K D 1




29 Only Sol 28 Figure Shows Three Vectors A B And C Where R Is The Midpoint Of Pq Physics Motion In A Plane Meritnation Com
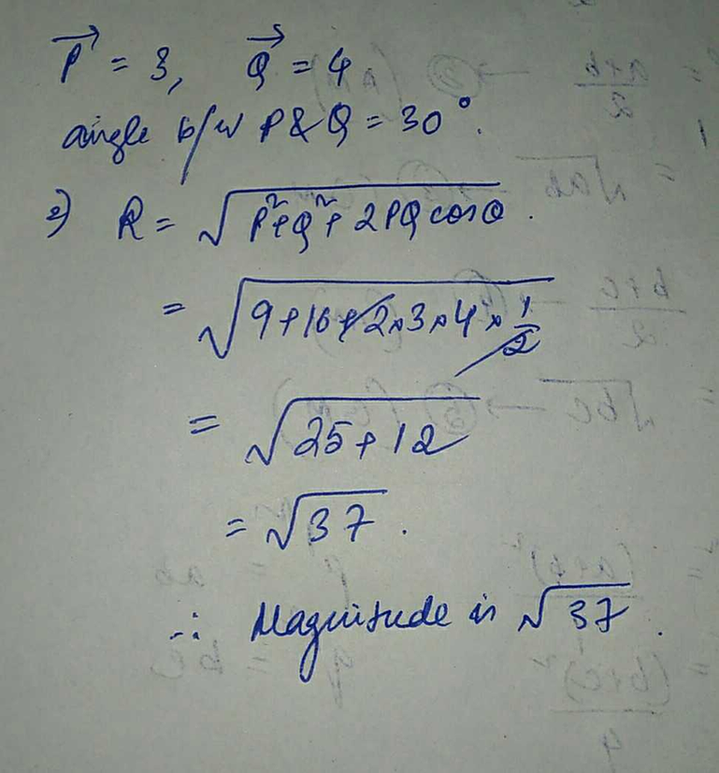



Two Vectors P And Q Have Magnitudes 3 Units And 4 Units Resp Scholr




If Vector P I J K And Q I 2j K Find A Vector Of Magnitude




Given P Q R If Vector P Vector Q Vector R Then The Angle Between Vector P And Q Is Theeta1 If Vector Brainly In



If P And Q Are Points With Coordinates 2 1 And 3 4 What Are The Coordinates Of Point R Such That Pr Is 2 5 Of Pq Quora




What Is The Angle Between P Q And P Q Youtube




If Vector P I J K And Q I 2j K Find A Vector Of Magnitude



O Is The Origin Op P And Oq Q Z Is A Point On Pq Such That Pz Zq 5 2 How To Work Out In Terms




The Resultant Of Two Vectors Vec P And Vec Q Is Vec R If Vec Q Is Doubled Then Youtube
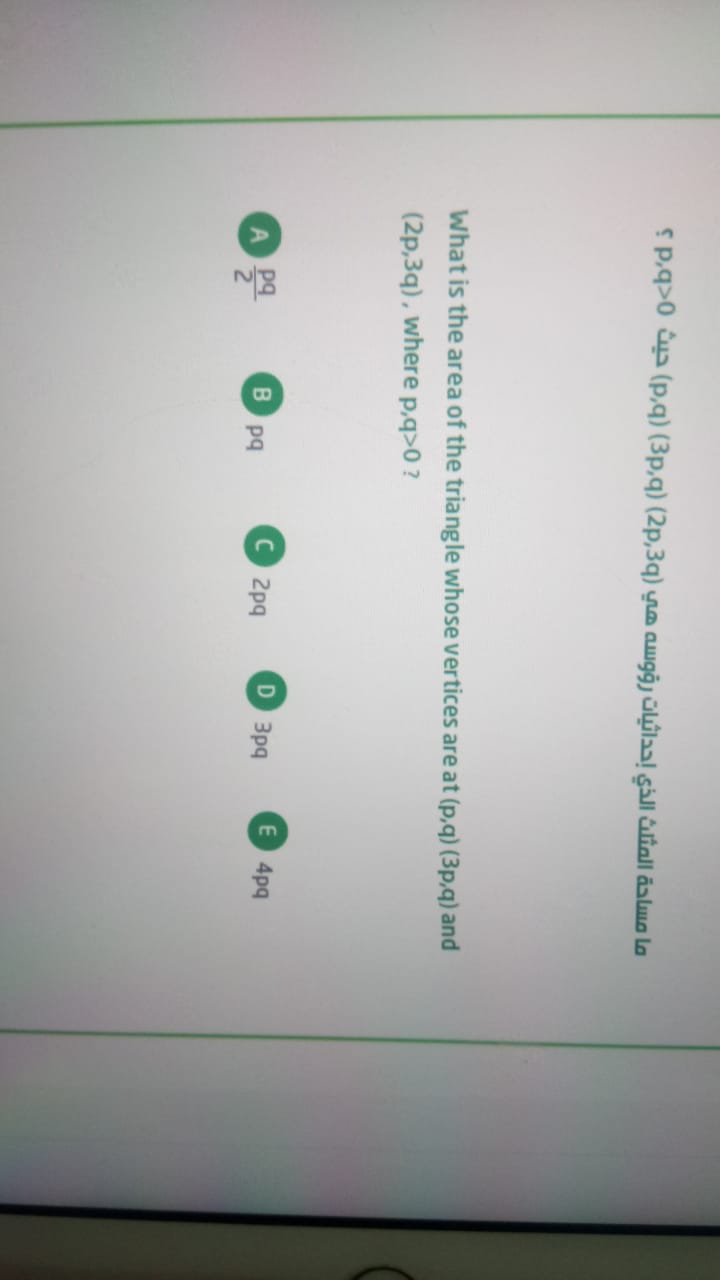



Answered What Is The Area Of The Triangle Whose Bartleby




Find Angle Between P Vector And Q Vector If Resultant Is Given By R 2 P 2 Q 2 Physics Topperlearning Com 40y2cnxx




Copy Of Chapter 01



At What Angle Do The Forces P Q And P Q Act So That The Resultant Is 3p 2 Q 2 Sarthaks Econnect Largest Online Education Community




P Q R And P Q C Then Q Is P Q R Are Vectors




Vector Geometry



The Resultant Of The Vector P And Q Is Perpendicular To The Vector P What Is The Angle Between P And Q Quora




If Vecp Vecq Pq Then Angle Between Vecp And Vecq Is
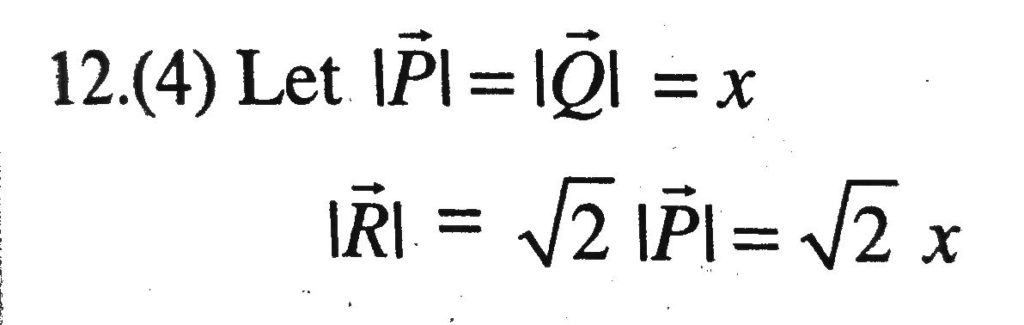



Three Vector P Q R Are Such That P Q R 2p And P Q R 0 The Angle Between P And Q Q And R And



Q Tbn And9gcr3h3a3p6js1bidhcruqoo90yfp Yfiwxypcajzkwyvppy2pqmo Usqp Cau




If P Q P Q Then




At What Angle Two Forces P Q And P Q Act So That Resultant Is I Sqrt 2 P 2 Q 2 Youtube




If P Q R And P Q Sqrt 3 And R 3 Then The Angle Betwe




Example Using Vectors To Find The Angles Of A Triangle Youtube




Can Anyone Explain Why It Is P Q Not P Q Maths



The Resultant Of Two Forces P And Q Is Equal To Q 3 And It Makes An Angle Of P 6 With The Direction Of P How Do You Show That P Q Or 2q




The Angle Of Inclination Between The Vectors P And Q Is Theta If Vectors P And Q Are Interchanged Physics Physics And Mathematics Meritnation Com




Magnitude And Direction Of Vectors




Two Forces P And Q Are In Ratio P Q 1 2 If Their Result Scholr




If P Q P Q And O Is The Angle Between P And Q Then A 0 00 B 0 900 C P 0




Given That P Q R If Vec P Vec Q Vec R Then The Angle Between Vec P And V Youtube




A The Column Vectors P And Q Are Defined By P Chegg Com




How To Prove That Non Zero Vectors P Q P Q If They Re Perpendicular Quora



1




8 4 Vectors A Vector Is A Quantity That Has Both Magnitude And Direction Vectors In The Plane Can Be Represented By Arrows The Length Of The Arrow Ppt Download
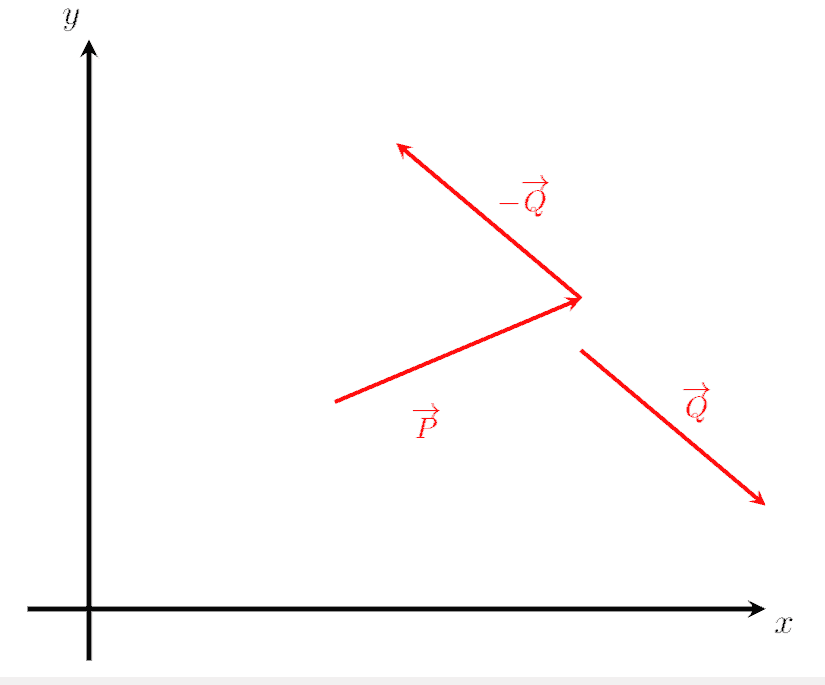



Vector Subtraction Explanation Examples




What Is The Angle Between P And The Resultant Of P Q And P Q Youtube




Euclidean Distance Wikipedia



0 件のコメント:
コメントを投稿