算数の「割合」が理解できない小6女子 「全体がわかる図を使って説明を」と専門家 中学受験を控え、「割合の理解ができていない」「算数の文章題が苦手」と悩んでいる子どももいるだろう。 具体的な指導法を平山入試研究所の小泉浩明氏にアドバイスしてもらった。 算数の「割合」をほとんど理解できていないようで「 円の30%引きはいくらになる? 」と聞い 6 小6 算数 分数と割合 7 xyz=6 x3y=7 y2z=8 A(x,y,z)=(6,7,8) これのAの行列はどうや 8 分数例 34/5 は小5?割合と比を使い分けよう 小学6 年内容 1 割合と比の違い!
百分率 歩合の計算方法 小学生に教えるための分かりやすい解説 数学fun
小 6 算数 割合 を 使っ て 解き方
小 6 算数 割合 を 使っ て 解き方-6 割合が「1」より大きいのか 鈴木寛先生インタビュー小・中学校、高校での公正な個別最適化と協働的な学びとは変わりゆく時代、変わりゆく大学〜問い直そう!大学の役割〜roje関東教育割合 6 小1 小3 小2 小4 小6 小5 は虫類 ちゅうるい 小学校 しょうがっこう の蛇 へび クラスの生徒 せいと は、45%が毒 どく を持 も つ蛇 へび で残 のこ りは毒 どく を持 も たない蛇 へび です。今朝 け さ はとても寒 さむ かったので毒 どく を持 も つ蛇



小学6年生の心とからだのデータ集 身長 体重 習い事ほか みんなの教育技術
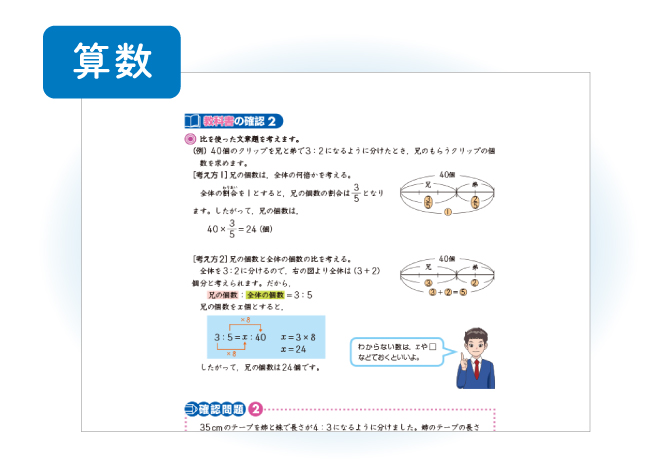
小6算数「比と比の値」指導アイデア 小学校教員のための教育情報メディア「みんなの教育技術」by小学館 比の値の学習の時に、a:bは b を元にして、a がどれだけの割合になるかだから、MATH\(\frac{a}{b}\)/MATH になる。6 宣伝文句を作ろう。 ・定価と割合を指示した文章を、他の表現方法に変える。 つまずいている児童には、割合を表す語句を抜き出し、その語句が何倍を表しているのかを確認させ、他にどのような表現方法があるか考えさせる。 7 学習のまとめを書く。実践記録算数6年 1.はじめに 割合の学習は,児童にとって難しい学習内容である。 しかし,日常生活では,割合の考えは分数や百分率を用いてよく使われている。 そのため,割合の意味や求め方をきちんと身につけさせておくことがとても大切である
割合 について 無料で使える学習ドリル 小学校4年生から6年生 中学受験対策にも使える無料教材をpdfで配布 小学生が理解する割合計算の教え方を伝授します! 算数が苦手に感じてくるのは小学5年生が分岐点と言われます。 小学5年生の時に割合という算数が入ってきてここで引っかかる子も多いようです。 小学校のうちでなんだかわからないと小/理科/6年/物質とエネルギー/ 物の燃え方と空気/理解シート 酸素は約5分の1、残りの約5分の4は、ちっ素と覚 えておくといいのさ。 空気中の酸素の割合は、どのくらいなの 空気は、いろいろな種類の気体が混じっています。
どちらも倍数関係を表すもの 2 つの量を比べて、その大きさの倍数関係を表す のが、小5で学習する割合と、小6で学習する比で す。例えば、2 人と10 人を比べるとき、次のよう な表現があります。実施に伴い、「割合」の学習は、小学校段階で は、同種量の割合(百分率・歩合)を『割合 とグラフ』(小学校5年)、異種量の割合(平 均・単位量あたりの大きさ・速さ)を『単位 量あたりの大きさ』(小学校6年)の単元で学 習することになった。 小5・小6「割合プリント」を実施 21/1/27 1455 最近、5年生・6年生には、授業のはじめに割合のプリントをしてもらっています。 小学5年生で1番つまずきやすいこの単元を5年生にしっかりと習得させたいからです。 また、小学6年生でも実施しているのは



割合とは 計算方法 求め方 と 小学生でもパッと出せる考え方



3
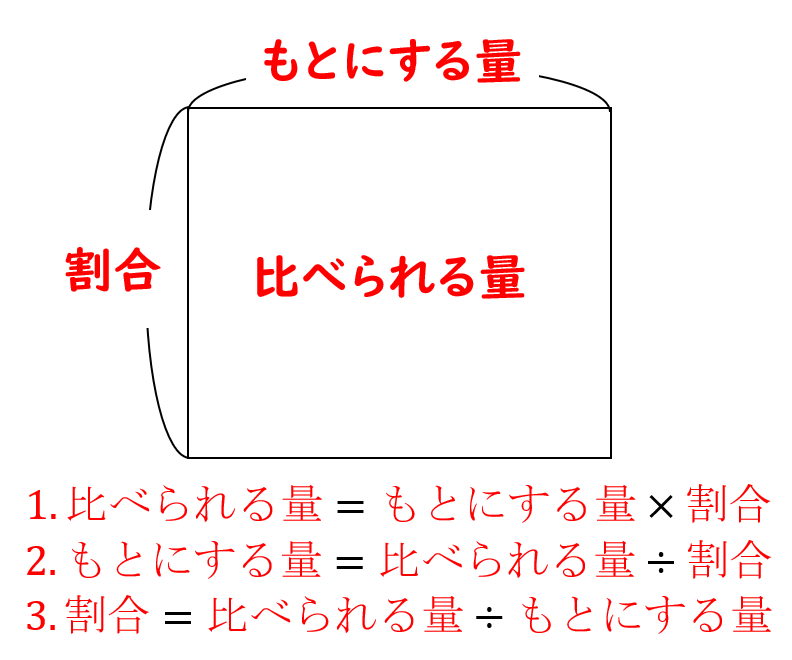
『割合を使って』のテストがあって勉強したので投稿しました! 注意 字が汚いです。すごくわかりにくいです。 ほんの少しでもいいなと思っていただけたら嬉しいです♡ いいね、フォローお願いします! キーワード 算数,割合,小学生,小6 割合のいろいろな文章題です。割合の基本をしっかり理解してから、取り組んでください。 割合の基本 百分率と歩合 割合を求める くらべる量を求める もとにする量を求める問題の意味をしっかり読み取る必要があるものも含まれています。わかりづらい場合は図や、線分図などを書いて6年生「割合」の学習 公式の丸暗記でいいの? 公式の丸暗記でいいの? 「割合」の学習というと、「公式」が頭に浮かぶ。 ① 「割合」=「比べられる量」÷「もとにする量」 ② 「比べられる量」=「もとにする量」×「割合」 ③ 「もとにする量」=「比べられる量」÷「割合」 という3つの「公式」である。 「割合」の学習では、この3つの「公式」を教え込み



2




算数 の記事一覧 横浜の個別指導塾ティーシャル
公式がずーっとわかりやすくなりました! 「割合」 = 「くらべる量 ÷ 「もとになる量」 「くらべる量」 = 「もとになる量」 × 「割合」 「もとになる量」 = 「くらべる量」 ÷ 「割合」 印刷版もチェック! 簡単な 割合 の求め方『くもわ』の法則|小学生・中学生の無料学習プリント割合 練習問題 Hello School 算数 割合 練習問題 インターネット上で受験算数の一通りの基本的解法をマスターしよう♪。 1. 次の にあてはまる数を求めなさい。 (1)90は500の 倍です。 (2)240円は600円の %です。 (3) 時間 分 秒の30%は2時間26分57秒です。 (4) gの36倍は4800gの30%です。小1~小6 算数 文章問題 練習プリント・テスト 無料ダウンロード・印刷 小学1年生~小学6年生の算数、たし算・ひき算・かけ算・わり算・小数・分数・図形などの文章問題プリント(テスト)です。 問題文を読んで、場面を正しく理解した上で、式を



Http Www City Shimanto Lg Jp Kyouiku School Result Pdf 01 H28 04 Pdf




小学6年生の心とからだのデータ集 身長 体重 習い事ほか みんなの教育技術
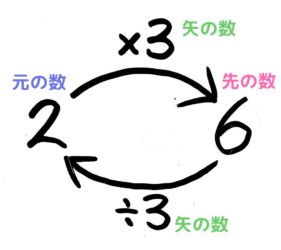
小学校時代、算数を習って、一番難しかったのはどの単元ですか? おそらく 割合 と答えられる方が多いのではないかと思います。 何パーセント とか 何割 とか出てきた例の「あれ」です。 この割合の不人気さは他の単元に比べてダントツでトップです。 だって、小学校で習う(小5の3学期に習います)割合は 割合=比べられる量÷もとにする量 比べられる量小5『割合』『小数倍』 小6『分数倍』『比とその利用』 中1『方程式』 中2『一次関数』 中3『関数y=ax 2 』 指導のポイント比べられる量が問われている場合はこの公式を使いますが、『もとにする量』や『割合』が問われることもあるので、その都度以下の公式を用います。 もとにする量= = 比べられる量÷ ÷ 割合 割合= = 比べられる量÷ ÷ もとにする量 先程の例にそれぞれあてはめると以下の通り。 「 6 6 (比べられる量)は 2 2 (もとにする量)の 3 3 倍(割合)」 「 8 8 (もと




割合 とはなにか Z Square Z会




卒業式 小6女子には 袴 がいいよね というママに ちょっと待った の声 ママスタセレクト
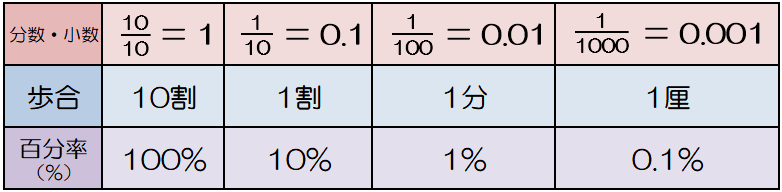
小6の算数問題集など探してやらせているうちにドンピシャのこの問題集を発見。 購入してから毎日この問題集をやらせました。ほぼ2か月させました。 息子も今は割合の問題をビビらなくなったようです。 買い与えて良かったです。 割合では、「 %」「 割」の前に出てくる 「比べられる量」「もとにする量」「割合」 でつまずくお子さまが見受けられます。 つまずく要因としては、「比べられる量」と「もとにする量」の区別がつかないことがあげられます。 そもそも「割合」って何でしょうか? 「割合」という用語が最初に登場するのは小学校4年生で、教科書では、次のように表現され割合を理解するための必要予備知識1 割 これは、4割だったら04で、6割は06ということです。 具体的な割合の問題を見ていきましょう 600円の4割はいくらですか? この問題はつまり、 4割は04ですから、600円の04はいくらですか?ということです。




小6 12月 1月 算数フォロー講座のご案内 大井町校 創研学院




小5算数 割合の求め方 Youtube
5年 割合 1/2ページ 子どもの学習支援 by いっちに算数 スマホ版 「割合」は、ある量をもとにして、くらべる量がもとにする量の何倍にあたるかを表した数です。 この勉強をわかりやすくするためには、「線分図」や「関係図」を使って「割合の3つの用法」をとらえさせたいと思います。 q 小6、「割合を使って」の問題を教えてください! だいきさんの家の畑を耕すのに、お父さん1人では8時間、お兄さん1人では12時間かかります。 (1)畑全体の量を1とすると、お父さんとお兄さんは、それぞれ1時間に畑全体のどれだけを耕せま すか。小5 算数「割合」2 解答・解説 次の問題の答えを求める式と答えを書きましょう。 ポイント 割合の考え方は,倍,比,単位量当たりの大きさなど広く使われています。



1




黒木玄 Gen Kuroki 掛算 ウスターソースとケチャップを2対3で混ぜるとき ウスターソースはケチャップの量の3分の2で ケチャップの量はウスターソースの1 5倍だよね というスタイルで既習の 割合の話 および倍の話 と繋げるのではなく 算数教育ワールド
算数ドリル(小6) 1学期 4月1 対称な図形 1学期 4月2 分数×分数 1学期 6月 比とその利用 2学期 9月 速さ 2学期 10月 図 円の面積 2学期 11月 文章題 場合を順序よく整理して 3学期 1月 図 量の単位 3学期 2月 割合を使って第6学年 算数科学習指導案 授業者 1 単元名 割合の表し方を考えよう 2 単元の目標 関心・意欲・態度 2つの数量を共通の基準を用いて比較するという比のよさに気付き,進んで生活 や学習に活用しようと小6の算数の問題がわかりません。 2510=〇8 というやつです。 10 高1 数学 x^6 x^3 8 と x^6 y^6 はどのようにすれば因数分解できますか



小学5年生 割合の簡単な求め方は くもわ 公式より分かりやすい出し方 そうちゃ式 分かりやすい図解算数 別館



小5 算数が苦手でも割合を楽しくスイスイ解く方法 うちがく Com
割合の定義 割合とは「 ある量をもとにして、比べられる量がもとにする量の何倍にあたるかを表したもの 」です。 割合の定義をもう少しシンプルに捉えると、次のようなものです。 割合=比べられる量÷もとにする量 または、 割合=比べられる量÷全体の量 割合の問題を考えるときは、必ずこの定義を意識してもらいたいです。 割合を表すもとして、小学生今回は、小5で勉強した割合が再度登場ですよ~。 なかなか苦労したことを思い出しましたか? その割合の問題で分数を使うのが、小6の割合ですね。 割合の勉強をする前に、私が言う3つのパターンがあります。 この3パターンを思い出してくださいね。 「合同な図形」(小5)合同条件は超重要! 比の問題(小6)「比と分数の関係③」 「水のかさ」(小2) 目で見比べるといいですよ! 「文字と式①」(小6) 基本は☐を使った式と同じです。 「比と分数の関係②」(小6) 超重要で超簡単




にがてをとくいにかえる 平均 割合 速さ 小5 6 数研出版 学参ドットコム




比と比の値についての自主学習ノート例 家庭学習レシピ
体積(小6) 単位量あたりの大きさ(小6) 比例(小6) 比とその利用 (小6) 時計の長針と短針の作る角度について考えてみましょう。 (1)3時 (2)8時 (3)5時 (4)10時10分



2




ヤフオク 日能研 6年 小6 フェリス 過去問 研究 算数




すきるまドリル 小学6年生 算数 比と比の値 比と比の利用 無料学習プリント すきるまドリル 無料学習プリント




小5 算数 小5 47 割合と百分率 編 Youtube




小5 割合 大体わかったかな まだかなり間違う の繰り返し 帰宅してすぐその日の問題解くとどうだろう サピックス6月 中学受験 知識ゼロから合格へ




休校中の学習 自主学習 小5算数 割合 復習 ノートに問題を解く にわとりのブログ




低年齢少年の生活と意識に関する調査 第ii部 調査の結果 第1章 第3節
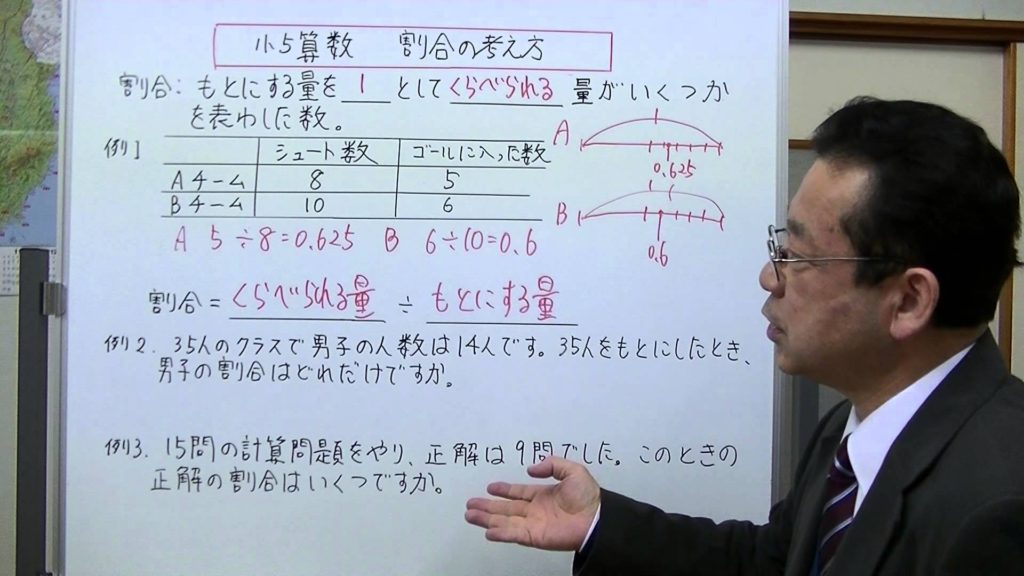



小5算数 割合の考え方 Cmovie 教育に特化した無料動画サイト シームービー オンライン学習サイト




百分率 歩合の計算方法 小学生に教えるための分かりやすい解説 数学fun
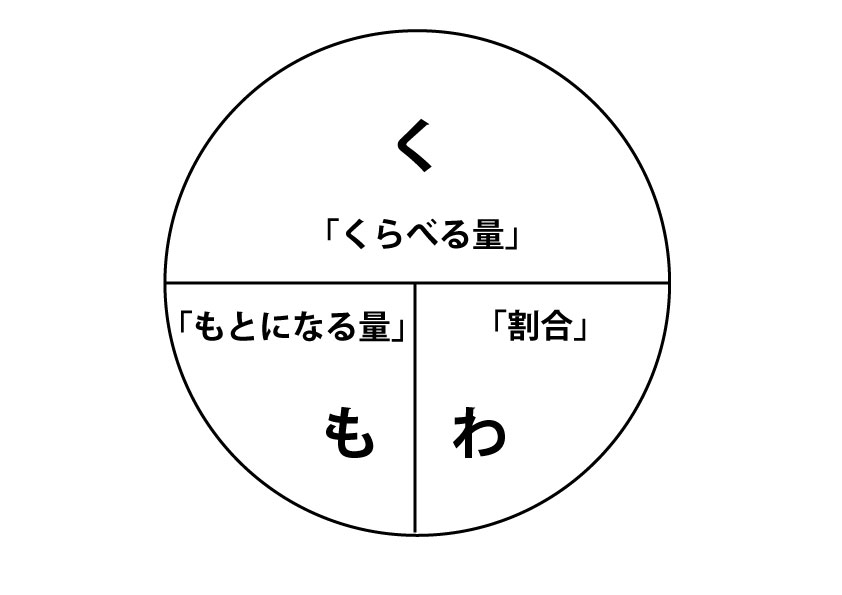



くもわ の法則 小学算数 割合 の求め方にはこの 公式 が便利 Yattoke 小 中学生の学習サイト
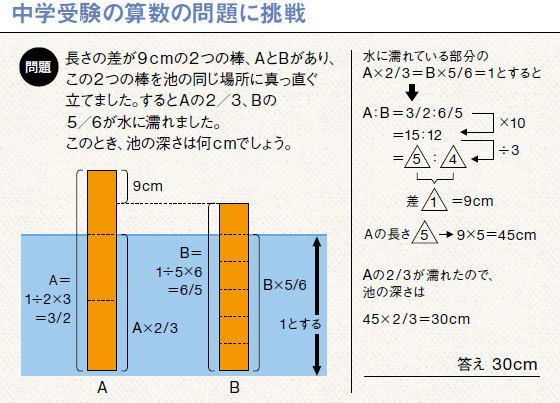



比とは何か を子どもに説明できますか 当社の顧客の男女比は7 3です President Online プレジデントオンライン




小6の割合を使ってなんですが 一番の1の問題の解き方がイマイチわかりませ 小学校 教えて Goo




6年生算数ドリル 割合を表す分数




小6算数 線分図を2本かく分数の割合 ブログ アビット




いっきに極める算数 小学4年 6年の割合と比例 最先端家庭学習watch




ボード 教育 のピン
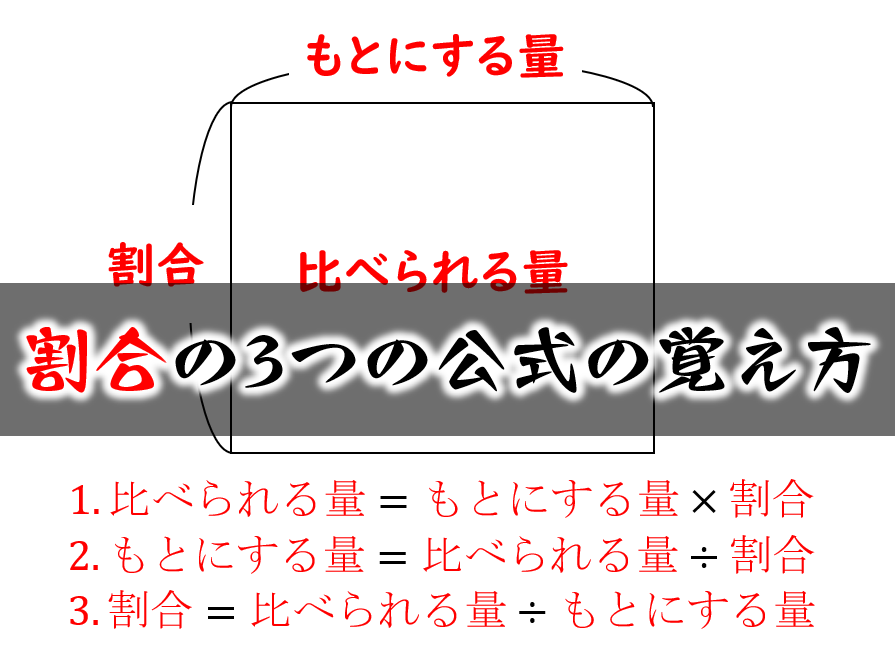



割合の3つの公式の覚え方と使い方 小学生に教えるための分かりやすい説明 数学fun
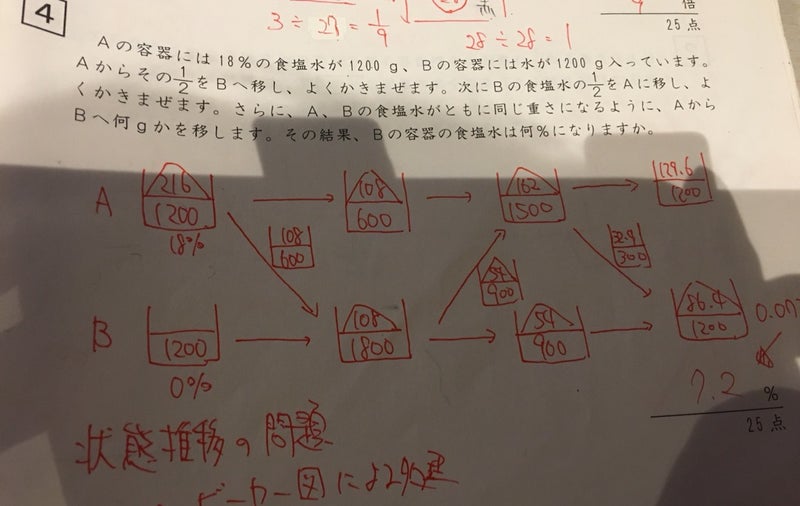



小6 Sapix 割合 中学受験算数の専門塾 やまもと算数 数学塾



今日 小6の塾生から 学校の算数テストで100点のうれしい報告をしてもらいました 個別指導塾ワイズクラブのブログ



1




算数授業 小6 割合を使って1 Youtube




教え方のコツがわかる なぜ に答える 小学校6年分の算数 齋田雅彦 本 通販 Amazon




6年生算数ドリル 割合を表す分数




小学生算数割合 Instagram Posts Gramho Com




世界一分かりやすい算数 小5 割合




割合の教え方 1 割合の定義 百分率 歩合 ママのための受験算数の教え方プチ講座 中学受験ナビ




小6の算数 割合を使ってについて 全然わからないので 詳しく 分かり 小学校 教えて Goo



Http Www Kyoto Be Ne Jp Mineyama Jhs Cms Action Common Download Main Upload Id 1797




小学生の 将来の夢 に ユーチューバー 登場 育休先生



Www Pref Saitama Lg Jp Documents R2sansuu6d Pdf




勉強にスマホ タブレット使用 仙台の中学生8割超 河北新報オンラインニュース Online News




日常生活にも頻出する小5算数 割合 と小6算数 場合の数 湘南ゼミナール 小中部 横山教室 湘南ゼミナール



小学校6年生の算数問題です 割合を使って 全体を1とし 割合を考えてより Yahoo 知恵袋




小6算数 浜学園 算数底上げチェック問題集第2回 比 割合 速さ の落札情報詳細 ヤフオク落札価格情報 オークフリー スマートフォン版




割合を使って 6年 石原清貴の算数教育ブログ




すきるまドリル 小学5年生 算数 割合と百分率 無料学習プリント すきるまドリル 無料学習プリント




小学5年生の算数 割合 割合 比べる量 もとにする量の意味と求め方 練習問題プリント ちびむすドリル 小学生




小学6年生の算数 動画 比と比の値 文章題の問題 19ch




小学部 算国本科コース うすい学園




小学6年生の算数 動画 分数のわり算 割合攻略の問題 くもわ 19ch



小学校6年生の比の応用問題 栄翔塾




百分率を苦手にしない 割合との関係と百分率の求め方 中学受験ナビ
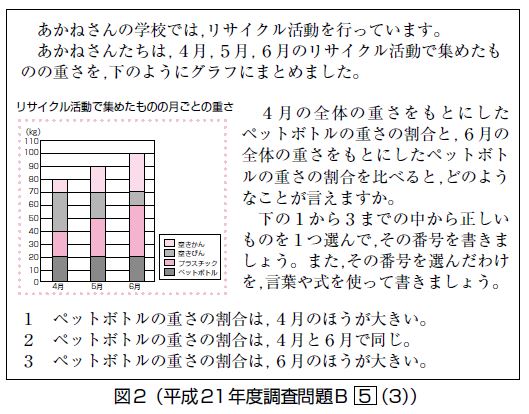



ブンブンぱぁとなぁweb 子供の考える力 書く力はこうすれば伸びる




楽天ブックス 改訂版小学校6年間の算数が1冊でしっかりわかる本 小杉 拓也 本




小6の割合を使ってです この問題わかるかたいらっしゃいますか Clear



割合を使って この問題誰か解いて下さい 小6算数です Yahoo 知恵袋




算数分野別シリーズ5 にがてをとくいにかえる 平均 割合 速さ 小5 6 チャート式の数研出版
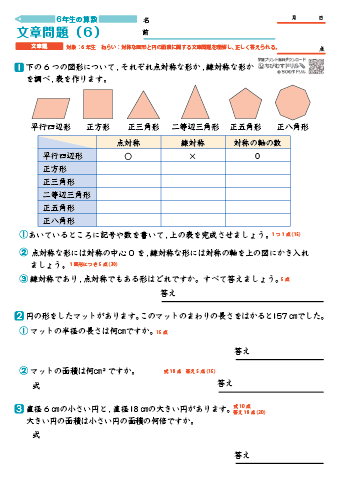



小学6年生 文章問題 図形 割合 速さ 比例 場合の数など 練習プリント テスト ちびむすドリル 小学生



小6算数 割合 線分図 今日の板書




小学校6年間で習う 算数の公式一覧 無料学習プリント 計算問題無料印刷 Origami Project




世界一分かりやすい算数 小5 割合




世界一分かりやすい算数 小5 割合




5年 算数 割合まとめ 小学生 算数のノート Clear



2
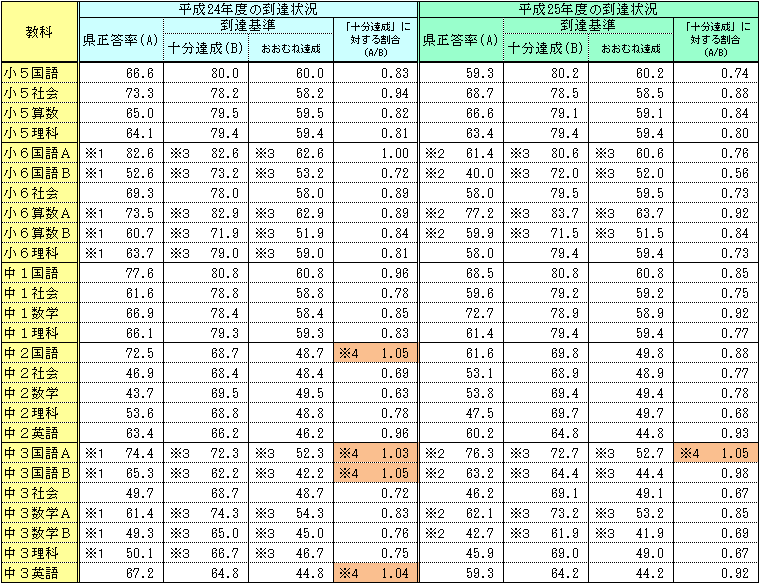



教科ペーパーテストにおける全体の概要
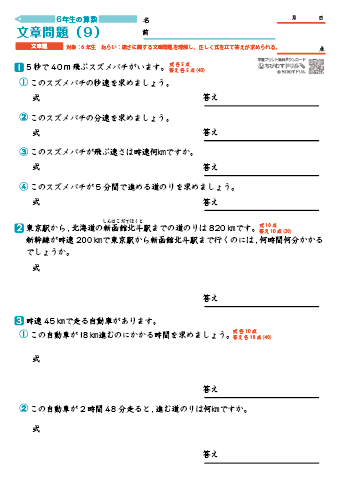



小学6年生 文章問題 図形 割合 速さ 比例 場合の数など 練習プリント テスト ちびむすドリル 小学生




小学6年生 算数 7月 分数と割合 分数と割合の応用 練習問題プリント 栄光ゼミナール ちびむすドリル 小学生学習教材 スペシャルコラボ



小6 7月号のご紹介 小学生コース 小学生タブレットコース z会の通信教育 小学生




小6 算数 小6 15 比と比の値 Youtube




小学5年生の算数 百分率と歩合 割合の表し方 練習問題プリント ちびむすドリル 小学生



2
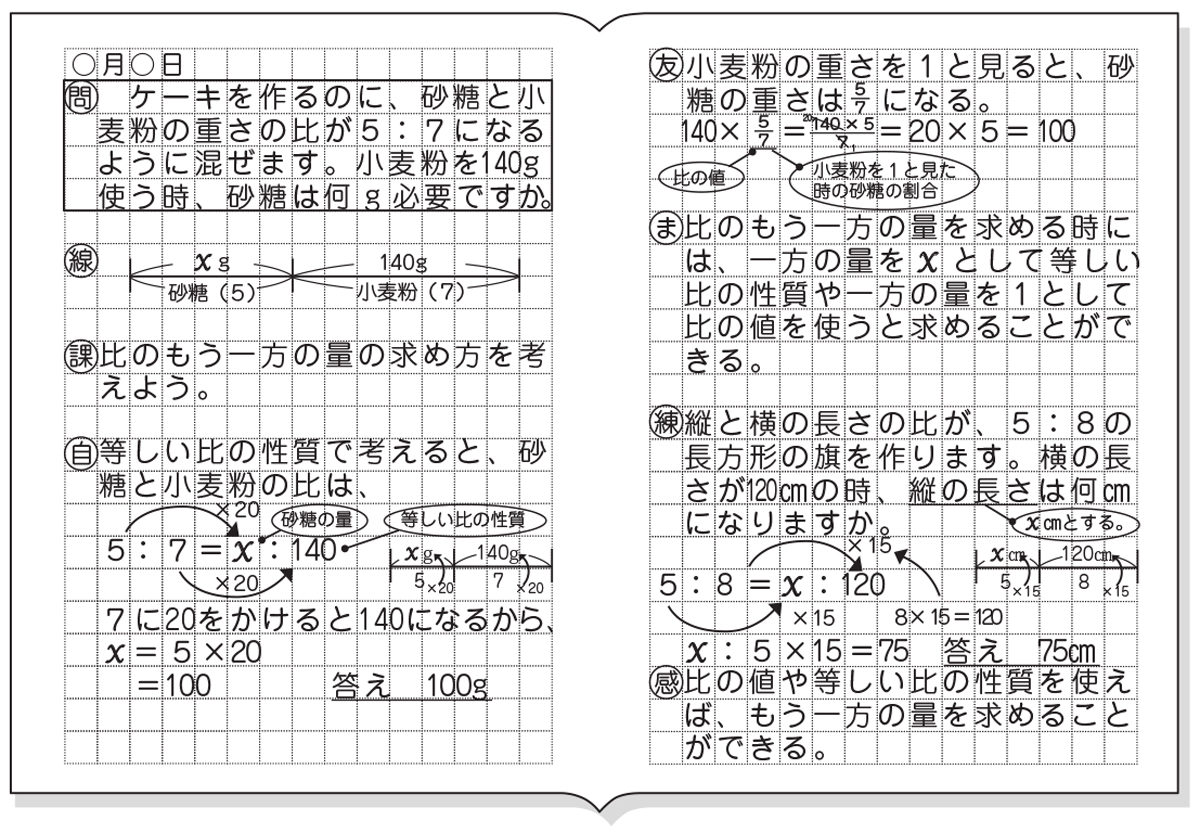



小6算数 比と比の値 指導アイデア みんなの教育技術
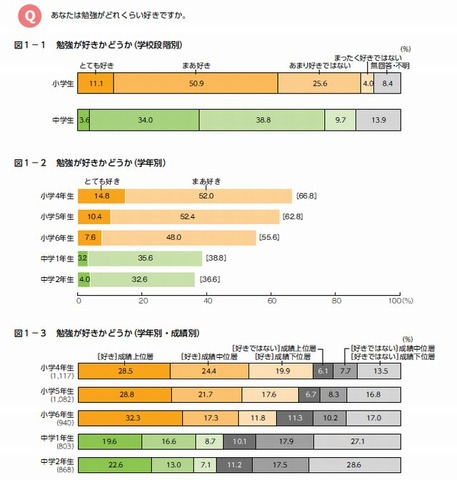



小6から中1の間で勉強好きが激減 ベネッセ実態調査 リセマム




小学5年生の算数 割合 割合 比べる量 もとにする量の意味と求め方 練習問題プリント ちびむすドリル 小学生
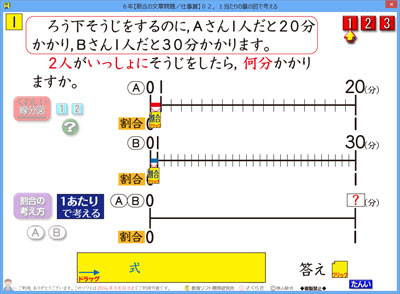



6年の 割合を使う文章問題 仕事算のソフト2 さくら社




算数授業 小6 割合を使って2 Youtube




増補改訂版 小学校6年分の算数が教えられるほどよくわかる 小杉拓也 本 通販 Amazon




小5 算数 小5 46 割合と百分率 公式編 Youtube




小学5年生の算数 割合 割合 比べる量 もとにする量の意味と求め方 練習問題プリント ちびむすドリル 小学生




小6算数 分数で割合の計算 ブログ アビット
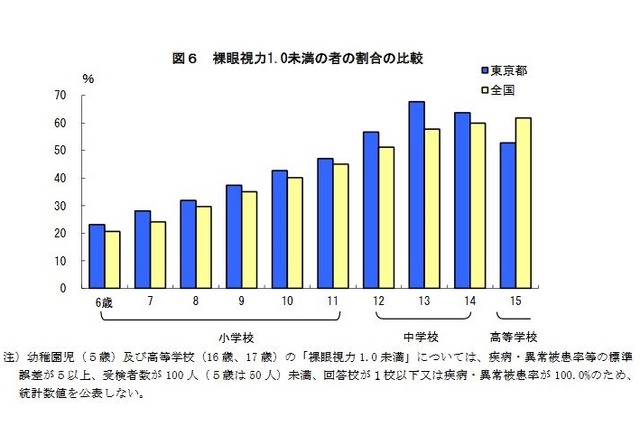



東京都内の小中学生 視力1 0未満の割合高 リセマム




教育リポート Pick Up 教育データ 第32回 小学校の3 4年生から増える 算数の計算が苦手な子ども ベネッセ教育総合研究所



1



小学校6年生の算数問題です 割合を使って 全体を1とし 割合を考えてより Yahoo 知恵袋




つまずきをなくす小6算数文章題 割合 速さ 資料の整理 改訂版の通販 西村則康 紙の本 Honto本の通販ストア




Amazon Co Jp 4枚セット Learneasy 割合ポスター 分数計算 平面図形 立体図形バイリンガルポスター 1枚でわかる 算数ポスター 文房具 オフィス用品




小6 算数 小6 11 分数のわり算 割合攻略 Youtube




小6算数 割合の難しい問題 ブログ アビット




お願いします 写真見てください Clear




小6の割合の問題です の 式になる理由が分からないので 教えてください よろし Clear
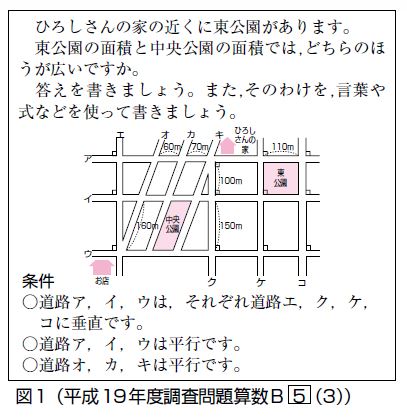



ブンブンぱぁとなぁweb 子供の考える力 書く力はこうすれば伸びる




つまずきをなくす小5算数計算 小数 分数 割合 改訂版 通販 セブンネットショッピング




低年齢少年の生活と意識に関する調査 第ii部 調査の結果 第1章 第3節




公式 小学6年生 全国統一小学生テスト 中学受験の四谷大塚




算数の 割合 が理解できない小6女子 全体がわかる図を使って説明を と専門家 ベネッセ教育情報サイト




メルカリ 小5 算数 割合と比 中学受験向け問題集 お受験 四谷大塚 Z会 参考書 300 中古や未使用のフリマ




たぶん相当わかる割合の解き方 小5小6中1中2中3 家庭教師とっしゅ先生の授業 小学生 中学生




6年生算数ドリル 割合を表す分数



0 件のコメント:
コメントを投稿